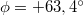„Mechanika - Rezgés kezdeti feltételekkel” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
|||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (2.1.49.) Pontszerűnek tekinthető $1\,\rm{kg}$ tömegű testre $F=–Dx$ erő hat. A rugóállandó: $D=25\,\rm N/\rm m$ . A $t=0$ pillanatban a kitérés $20\,\rm{cm}$, a sebesség $2\,\rm{m/s}$ és növekszik. | + | </noinclude><wlatex># (2.1.49.) Pontszerűnek tekinthető $1\,\rm{kg}$ tömegű testre $F=–Dx$ erő hat. A rugóállandó: $D=25\,\rm N/\rm m$ . A $t=0$ pillanatban a kitérés $+20\,\rm{cm}$, a sebesség $2\,\rm{m/s}$ és a nagysága növekszik. |
#: a) Mekkora a rezgés frekvenciája? | #: a) Mekkora a rezgés frekvenciája? | ||
#: b) Mekkora a rezgés amplitúdója? | #: b) Mekkora a rezgés amplitúdója? | ||
| − | #: c) Írja fel a helyzet-idő függvényt! Mekkora a kezdőfázis?</wlatex><includeonly><wlatex>{{ | + | #: c) Írja fel a helyzet-idő függvényt! Mekkora a kezdőfázis?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\omega=5\,\frac1{\rm s}$$ $$A=0,448\,\rm m$$ $$x(t)=\cos(\omega t+63,4^{\circ})$$}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A rezgés körfrekvenciája $\omega=\sqrt{D/m}=\sqrt{25} \frac1{\rm s}=5 \frac1{\rm s}$. A kezdőpillanatban a rezgés energiája részben mozgási és részben rugalmas helyzeti, kettejük összege viszont a teljes rezgési energia, amiből megkapható az amplitúdó (vagy a sebességmaximum): $$\frac12 mv_0^2+\frac12 Dx_0^2=\frac12 DA^2,$$ melyben $D$-t helyettesítve, a tömeggel egyszerűsítve és $\omega^2$-tel leosztva kapjuk: $$\frac{v_0^2}{\omega^2}+x_0^2=A^2=0,2\,\rm{m^2}$$ így $A=0,448\,\rm m$. A helyzet-idő függvényt $x(t)=\cos(\omega t+\phi)$ alakban keresve $x(0)=A\cos{\phi}=x_0$ és $\dot{x}(0)=-A\omega\sin{\phi}=v_0$ egyenleteket egymással elosztva $$\tan{\phi}=\frac{-v_0}{\omega x_0}= | + | <wlatex>A rezgés körfrekvenciája $\omega=\sqrt{D/m}=\sqrt{25}\,\frac1{\rm s}=5\,\frac1{\rm s}$. A kezdőpillanatban a rezgés energiája részben mozgási és részben rugalmas helyzeti, kettejük összege viszont a teljes rezgési energia, amiből megkapható az amplitúdó (vagy a sebességmaximum): $$\frac12 mv_0^2+\frac12 Dx_0^2=\frac12 DA^2,$$ melyben $D$-t helyettesítve, a tömeggel egyszerűsítve és $\omega^2$-tel leosztva kapjuk: $$\frac{v_0^2}{\omega^2}+x_0^2=A^2=0,2\,\rm{m^2}$$ így $A=0,448\,\rm m$. A helyzet-idő függvényt $x(t)=\cos(\omega t+\phi)$ alakban keresve $x(0)=A\cos{\phi}=x_0$ és $\dot{x}(0)=-A\omega\sin{\phi}=v_0=-2\,\rm{m/s}$ egyenleteket egymással elosztva $$\tan{\phi}=\frac{-v_0}{\omega x_0}=+2,$$ ebből $\phi=+63,4^{\circ}$</wlatex> |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. november 27., 15:51-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rezgések I. |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (2.1.49.) Pontszerűnek tekinthető
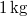 tömegű testre
tömegű testre 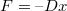 erő hat. A rugóállandó:
erő hat. A rugóállandó: 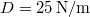 . A
. A  pillanatban a kitérés
pillanatban a kitérés 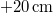 , a sebesség
, a sebesség 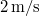 és a nagysága növekszik.
és a nagysága növekszik.
- a) Mekkora a rezgés frekvenciája?
- b) Mekkora a rezgés amplitúdója?
- c) Írja fel a helyzet-idő függvényt! Mekkora a kezdőfázis?
Megoldás
A rezgés körfrekvenciája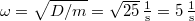 . A kezdőpillanatban a rezgés energiája részben mozgási és részben rugalmas helyzeti, kettejük összege viszont a teljes rezgési energia, amiből megkapható az amplitúdó (vagy a sebességmaximum):
. A kezdőpillanatban a rezgés energiája részben mozgási és részben rugalmas helyzeti, kettejük összege viszont a teljes rezgési energia, amiből megkapható az amplitúdó (vagy a sebességmaximum): ![\[\frac12 mv_0^2+\frac12 Dx_0^2=\frac12 DA^2,\]](/images/math/8/0/a/80a1f53286cf98cc57e26958c9833566.png)
 -t helyettesítve, a tömeggel egyszerűsítve és
-t helyettesítve, a tömeggel egyszerűsítve és 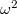 -tel leosztva kapjuk:
-tel leosztva kapjuk: ![\[\frac{v_0^2}{\omega^2}+x_0^2=A^2=0,2\,\rm{m^2}\]](/images/math/2/2/c/22cd90fa8dc84416356dabbfd4851baa.png)
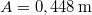 . A helyzet-idő függvényt
. A helyzet-idő függvényt 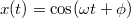 alakban keresve
alakban keresve 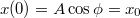 és
és 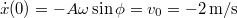 egyenleteket egymással elosztva
egyenleteket egymással elosztva ![\[\tan{\phi}=\frac{-v_0}{\omega x_0}=+2,\]](/images/math/8/4/f/84f19190261ac6062a8a10c154e7b8e3.png)