„Elektrosztatika - Elektromos potenciál” változatai közötti eltérés

A lap 2013. április 28., 15:06-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 2.
Gyakorlatok listája: Erőhatások elektromos erőtérben, elektromos térerősség Elektromos potenciál Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok Kapacitás, kondenzátorok. Elrendezések energiája Vezetőképesség, áramsűrűség Biot-Savart törvény, gerjesztési törvény Erőhatások mágneses térben Mágneses térerősség. Kölcsönös és öninduktivitás Az indukció törvénye, mozgási indukció Mágneses tér energiája. Váltakozó áram, eltolási áram
Elektrosztatika - Elektromos potenciál
Feladatok listája: Potenciál számítása a térerősségből Elektromos térerősség kiszámítása a potenciálból Töltésen végzett munka A potenciál változása egyenletesen töltött körlap tengelye mentén Párhuzamos végtelen síklapok potenciáltere Összeolvadt esőcseppek potenciálja Fém gömbhéjjal koncentrikusan körülvett töltött fémgömb esetén kialakuló potenciáltér Töltéssel ellátott koaxiális fémhengerek közötti potenciálkülönbség A potenciál töltött fémszállal koaxiális fémhenger esetén Vezető félgömb potenciálja a gömb középpontjában
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

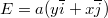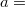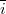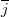Határozzuk meg az $\setbox0\hbox{$ E=a ( y\overline{i}+x\overline{j} ) $}% \message{//depth:\the\dp0//}% \box0%$ elektromos erőtér potenciálját, ha $\setbox0\hbox{$a=$}% \message{//depth:\the\dp0//}% \box0%$ állandó, $\setbox0\hbox{$\overline{i}$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$\overline{j}$}% \message{//depth:\the\dp0//}% \box0%$ az $\setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$y$}% \message{//depth:\the\dp0//}% \box0%$ tengely irányába mutató egységvektorok!
Végeredmény
$U=-axy+C$

Megoldás
Határozzuk meg az elektromos térerősség vektorát, ha a potenciál:
a)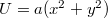 $\setb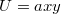ox0\hbox{$U=a(x^2+y^2)$}% \message{//depth:\the\dp0//}% \box0%$
b) $\setbox0\hbox{$U=axy$}% \message{//depth:\the\dp0//}% \box0%$
módon függ a koordinátáktól, ahol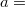 $\setbox0\hbox{$a=$}% \message{//depth:\the\dp0//}% \box0%$ állandó!
Végeredmény
a)
$\overline{E}=-2ax\overline{i}+2ay\overline{j}$
b)
$\overline{E}=-ay\overline{i}-ax\overline{j}$

Megoldás

@@ 4. sor: / 4. sor: @@
 | tárgynév    = Kísérleti fizika gyakorlat 2.
 | gyaksorszám = 2
-| témakör     = Elektrosztatika - Elektromos potenciál|Elektromos potenciál
+| témakör     = Elektrosztatika - Elektromos potenciál
 }}
 == Feladatok ==
 {{:Elektrosztatika példák - Potenciál térerősségből való kiszámolása}}{{Megoldás|link=Elektrosztatika példák - Potenciál térerősségből való kiszámolása}}
 {{:Elektrosztatika példák - Elektromos térerősség potenciálból való kiszámolása}}{{Megoldás|link=Elektrosztatika példák - Elektromos térerősség potenciálból való kiszámolása}}