„Mechanika - Lebegés” változatai közötti eltérés

A lap 2012. december 2., 14:53-kori változata (lapforrás) Gombkoto (vitalap | szerkesztései) (Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”)		A lap jelenlegi, 2012. december 2., 14:58-kori változata (lapforrás) Gombkoto (vitalap | szerkesztései)
8. sor:		8. sor:
	}}		}}
	== Feladat ==		== Feladat ==
−	</noinclude><wlatex># (*6.22.) Két, azonos amplitúdójú rezgés, melyek frekvenciája $f_1=50\,\rm{Hz}$ és $f_2=60\,\rm{Hz}$ egyszerre kezdi meg rezgését az egyensúlyi helyzetből. Mikor lesz legelőször ismét azonos a kitérésük?</wlatex><includeonly><wlatex>{{Útmutatás|content=útmutatás szövege}}{{Végeredmény|content=eredmény szövege}}</wlatex></includeonly><noinclude>	+	</noinclude><wlatex># (6.24.) Két egyirányú harmonikus rezgés eredője: $x(t)=A\cos(2t)\cos(50t)$, ahol $t$ másodpercekben értendő. Mekkora az összetevő rezgések frekvenciája, és mekkora a lebegés frekvenciája?</wlatex><includeonly><wlatex>{{Útmutatás|content=Alakítsuk át a függvényt trigonometrikus függvények összegére!}}{{Végeredmény|content=$$f_l=0,636\,\rm{Hz}$$}}</wlatex></includeonly><noinclude>
	== Megoldás ==		== Megoldás ==
−	<wlatex>megoldás szövege</wlatex>	+	<wlatex>Trigonometrikus azonosságot felhasználva a szorzat alak koszinuszok összegévé írható át, melyek frekvenciáját $\omega_1$-el és $\omega_2$-vel jelölve $$\frac{\omega_1+\omega_2}2=50$$ $$\frac{\omega_1-\omega_2}2=2$$ Ezt az egyenletrendszert megoldva $\omega_1=52\,\frac1{\rm s}$ és $\omega_2=48\,\frac1{\rm s}$, a lebegés körfrekvenciája pedig a kettő különbségéből $\omega_l=4\,\frac1{\rm s}$, azaz $$f_l=0,636\,\rm{Hz}$$ Érdemes megjegyezni, hogy a $w_l$ nem az eredeti alakból tévesen következtethető $2\,\frac1{\rm s}$, hanem ennek kétszerese, mivel a lassabban változó tényező egy szimmetrikus burkolót képez a gyorsan változó köré. Tehát a koszinusz egy periódusa alatt két "púpja" van, vagy más megfogalmazásban ennek a tényezőnek az abszolút értéke számít, aminek viszont fele akkora periódusideje van.</wlatex>
	</noinclude>		</noinclude>

---

A lap jelenlegi, 2012. december 2., 14:58-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája: Deriválás Integrálás Mozgástan Erőtan I. Erőtan II. Munka, energia Pontrendszerek Merev testek I. Merev testek II. Rugalmasság, folyadékok Rezgések I. Rezgések II. Hullámok
Mechanika - Rezgések I.
Feladatok listája: Rezgések pályaegyenlete Rugóra akasztott test Rezgés kezdeti feltételekkel Rezgés egyensúlyi helyzetből Rezgő testre rápottyanó Kosárba ejtett test Rugókra merőleges rezgés Inga kétféle rezgésideje Rezgés ferde rugóval Kiskocsik rugóval Függvényalak átalakítása Eredő rezgés adatai Adott eredő rezgés Azonos kitérés ideje Lebegés
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

1. (6.24.) Két egyirányú harmonikus rezgés eredője: 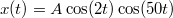, ahol másodpercekben értendő. Mekkora az összetevő rezgések frekvenciája, és mekkora a lebegés frekvenciája?

Megoldás

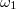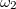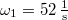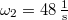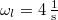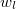Trigonometrikus azonosságot felhasználva a szorzat alak koszinuszok összegévé írható át, melyek frekvenciáját -el és -vel jelölve Ezt az egyenletrendszert megoldva és , a lebegés körfrekvenciája pedig a kettő különbségéből , azaz Érdemes megjegyezni, hogy a nem az eredeti alakból tévesen következtethető 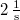, hanem ennek kétszerese, mivel a lassabban változó tényező egy szimmetrikus burkolót képez a gyorsan változó köré. Tehát a koszinusz egy periódusa alatt két "púpja" van, vagy más megfogalmazásban ennek a tényezőnek az abszolút értéke számít, aminek viszont fele akkora periódusideje van.