„Mechanika - Rezgések pályaegyenlete” változatai közötti eltérés
A Fizipedia wikiből
| 12. sor: | 12. sor: | ||
#: b) $x=A\sin{\omega t}$ ; $y=A\cos{2\omega t}$</wlatex><includeonly><wlatex>{{Útmutatás|content=Ejtsük ki az időkoordinátát.}}{{Végeredmény|content=$$y^2=4x^2\left(1-\frac{x^2}{A^2}\right)$$ $$y=A\left(1-\frac{2x^2}{A^2}\right)$$}}</wlatex></includeonly><noinclude> | #: b) $x=A\sin{\omega t}$ ; $y=A\cos{2\omega t}$</wlatex><includeonly><wlatex>{{Útmutatás|content=Ejtsük ki az időkoordinátát.}}{{Végeredmény|content=$$y^2=4x^2\left(1-\frac{x^2}{A^2}\right)$$ $$y=A\left(1-\frac{2x^2}{A^2}\right)$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: a) $$y^2=4A^2\sin^2{\omega t}\cos^2{\omega t}=4x^2(1-\sin^2{\omega t})=4x^2\left(1-\frac{x^2}{A^2}\right)$$ | + | <wlatex>#: [[Kép:kisfiz1gy-1.4.35M.svg|none|250px]]a) $$y^2=4A^2\sin^2{\omega t}\cos^2{\omega t}=4x^2(1-\sin^2{\omega t})=4x^2\left(1-\frac{x^2}{A^2}\right)$$ |
#: b) $$y=A(\cos^2{\omega t}-\sin^2{\omega t})=A(1-2\sin^2{\omega t})=A\left(1-\frac{2x^2}{A^2}\right)$$</wlatex> | #: b) $$y=A(\cos^2{\omega t}-\sin^2{\omega t})=A(1-2\sin^2{\omega t})=A\left(1-\frac{2x^2}{A^2}\right)$$</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. november 27., 15:09-kori változata
Feladat
- (1.4.35.) Határozzuk meg a pont
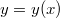pályaegyenletét, ha a koordináták időfüggése:
- a)
; 
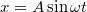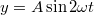
- b) ;
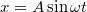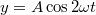
- a)
Megoldás
- a)
![\[y^2=4A^2\sin^2{\omega t}\cos^2{\omega t}=4x^2(1-\sin^2{\omega t})=4x^2\left(1-\frac{x^2}{A^2}\right)\]](/images/math/d/a/4/da45307cd96879a826369021459da913.png)
- b)
![\[y=A(\cos^2{\omega t}-\sin^2{\omega t})=A(1-2\sin^2{\omega t})=A\left(1-\frac{2x^2}{A^2}\right)\]](/images/math/8/f/0/8f06eb5880555a4b7c4beec47823b8bf.png)
-
