„Mechanika - Rezgések pályaegyenlete” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
|||
| 10. sor: | 10. sor: | ||
</noinclude><wlatex># (1.4.35.) Határozzuk meg a pont $y=y(x)$ pályaegyenletét, ha a koordináták időfüggése: | </noinclude><wlatex># (1.4.35.) Határozzuk meg a pont $y=y(x)$ pályaegyenletét, ha a koordináták időfüggése: | ||
#: a) $x=A\sin{\omega t}$ ; $y=A\sin{2\omega t}$ | #: a) $x=A\sin{\omega t}$ ; $y=A\sin{2\omega t}$ | ||
| − | #: b) $x=A\sin{\omega t}$ ; $y=A\cos{2\omega t}$</wlatex><includeonly><wlatex>{{Útmutatás|content=Ejtsük ki az időkoordinátát.}}{{Végeredmény|content=$$y=2x\sqrt{1-\frac{x^2}{A^2}}$$ $$y=A\left(1-\frac{2x^2}{A^2}\right)$$}}</wlatex></includeonly><noinclude> | + | #: b) $x=A\sin{\omega t}$ ; $y=A\cos{2\omega t}$</wlatex><includeonly><wlatex>{{Útmutatás|content=Ejtsük ki az időkoordinátát.}}{{Végeredmény|content=$$y=2x\pm\sqrt{1-\frac{x^2}{A^2}}$$ $$y=A\left(1-\frac{2x^2}{A^2}\right)$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: a) $$\frac y {2A}=\sin{\omega t}\cos{\omega t}=\frac xA\sqrt{1-\sin^2{\omega t}}=\frac xA\sqrt{1-\frac{x^2}{A^2}}$$ | + | <wlatex>#: a) $$\frac y {2A}=\sin{\omega t}\cos{\omega t}=\frac xA\pm\sqrt{1-\sin^2{\omega t}}=\frac xA\pm\sqrt{1-\frac{x^2}{A^2}}$$ |
#: b) $$y=A(\cos^2{\omega t}-\sin^2{\omega t})=A(1-2\sin^2{\omega t})=A\left(1-\frac{2x^2}{A^2}\right)$$</wlatex> | #: b) $$y=A(\cos^2{\omega t}-\sin^2{\omega t})=A(1-2\sin^2{\omega t})=A\left(1-\frac{2x^2}{A^2}\right)$$</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. november 26., 23:35-kori változata
Feladat
- (1.4.35.) Határozzuk meg a pont
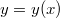 pályaegyenletét, ha a koordináták időfüggése:
pályaegyenletét, ha a koordináták időfüggése:
- a)
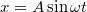 ;
; 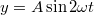
- b)
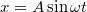 ;
; 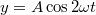
- a)
Megoldás
- a)
![\[\frac y {2A}=\sin{\omega t}\cos{\omega t}=\frac xA\pm\sqrt{1-\sin^2{\omega t}}=\frac xA\pm\sqrt{1-\frac{x^2}{A^2}}\]](/images/math/9/f/8/9f88a36938e70348b52f051ae19f6c71.png)
- b)
![\[y=A(\cos^2{\omega t}-\sin^2{\omega t})=A(1-2\sin^2{\omega t})=A\left(1-\frac{2x^2}{A^2}\right)\]](/images/math/8/f/0/8f06eb5880555a4b7c4beec47823b8bf.png)
- a)