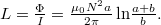„Magnetosztatika - Mágneses térerősség. Kölcsönös és öninduktivitás” változatai közötti eltérés
A Fizipedia wikiből
(→Feladatok) |
(→Feladatok) |
||
| 10. sor: | 10. sor: | ||
{{:Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása}}{{Megoldás|link=Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása}} | {{:Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása}}{{Megoldás|link=Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása}} | ||
{{:Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása2}}{{Megoldás|link=Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása2}} | {{:Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása2}}{{Megoldás|link=Magnetosztatika példák - Négyzetes toroid tekercs öninduktivitása2}} | ||
| + | {{:Magnetosztatika példák - B és H fluxusa mágneses anyag jelenlétében2}}{{Megoldás|link=Magnetosztatika példák - B és H fluxusa mágneses anyag jelenlétében2}} | ||
A lap 2013. április 26., 16:09-kori változata
Feladatok
- A mágneses indukció
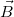 vektorára merőleges sík
vektorára merőleges sík 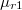 és
és 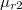 relatív permeabilitású anyagokat választ el egymástól. Tekintsünk egy hengert, melynek
relatív permeabilitású anyagokat választ el egymástól. Tekintsünk egy hengert, melynek  területű körlapjai párhuzamosak a határfelülettel! Határozzuk meg a
területű körlapjai párhuzamosak a határfelülettel! Határozzuk meg a 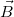 mágneses indukció és a
mágneses indukció és a 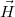 mágneses térerősség fluxusát erre a hengerre!
mágneses térerősség fluxusát erre a hengerre!
- Határozzuk meg egy
 oldalú, négyzet keresztmetszetű,
oldalú, négyzet keresztmetszetű,  menetű toroid tekercs öninduktivitását, ha a tekercs belső sugara
menetű toroid tekercs öninduktivitását, ha a tekercs belső sugara  !
!
- Határozzuk meg egy
 oldalú, négyzet keresztmetszetű,
oldalú, négyzet keresztmetszetű,  menetű toroid tekercs öninduktivitását, ha a tekercs belső sugara
menetű toroid tekercs öninduktivitását, ha a tekercs belső sugara  !
!
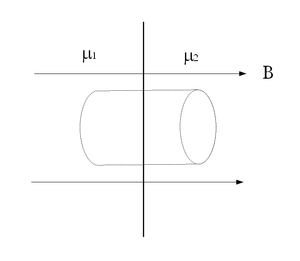
- A mágneses indukció
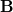 vektorára merőleges sík
vektorára merőleges sík 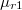 és
és 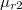 relatív permeabilitású anyagokat választ el egymástól. Tekintsünk egy hengert, melynek
relatív permeabilitású anyagokat választ el egymástól. Tekintsünk egy hengert, melynek  területű körlapjai párhuzamosak a határfelülettel! Határozzuk meg a
területű körlapjai párhuzamosak a határfelülettel! Határozzuk meg a 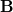 mágneses indukció és a
mágneses indukció és a 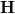 mágneses térerősség fluxusát erre a hengerre!
mágneses térerősség fluxusát erre a hengerre!
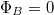
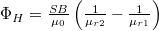
 mágneses térerősséget a tekercs belsejében a tengelytől mért távolság függvényében a gerjesztési törvénysegítségével, számoljuk ki ebből 1 menetre a fluxust, végül az
mágneses térerősséget a tekercs belsejében a tengelytől mért távolság függvényében a gerjesztési törvénysegítségével, számoljuk ki ebből 1 menetre a fluxust, végül az