„Mechanika - Adott eredő rezgés” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
|||
| 13. sor: | 13. sor: | ||
#: c) Mekkorára kell a második rezgés kezdőfázisát választani, hogy az eredő amplitúdó $7\,\rm{cm}$ legyen?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\phi_2=-90^{\circ}$$ $$A_2\approx5,2\,\rm{cm}$$ $$\phi_2=-53,6^{\circ}$$ vagy $$\phi_2=113,6^{\circ}$$}}</wlatex></includeonly><noinclude> | #: c) Mekkorára kell a második rezgés kezdőfázisát választani, hogy az eredő amplitúdó $7\,\rm{cm}$ legyen?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\phi_2=-90^{\circ}$$ $$A_2\approx5,2\,\rm{cm}$$ $$\phi_2=-53,6^{\circ}$$ vagy $$\phi_2=113,6^{\circ}$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>a) | + | <wlatex> [[Kép:Kfgy1-6-21M.svg|none|250px]]a) A forgóvektorok vagy a komplex amplitúdók ábrázolásából következik, hogy a második rezgés kezdőfázisa $-90^{\circ}$ kell legyen. |
b) Ugyancsak a kapott derékszögű vektorháromszög alapján $A_2^2+3^2=6^2$ (cm-ekben értve mindent), így $$A_2=\sqrt{27}\,\rm{cm}=3\sqrt3\,\rm{cm}\approx5,2\,\rm{cm}$$ | b) Ugyancsak a kapott derékszögű vektorháromszög alapján $A_2^2+3^2=6^2$ (cm-ekben értve mindent), így $$A_2=\sqrt{27}\,\rm{cm}=3\sqrt3\,\rm{cm}\approx5,2\,\rm{cm}$$ | ||
| − | c) | + | c) Ebben az esetben a vektorháromszög nem derékszögű, viszont minden oldala ismert, valamint az $\tilde A_1$ komplex amplitúdó $\phi_1$ fázisszöge is. Alkalmazva a koszinusz-tételt az $\tilde A_1$ és $\tilde A_2$ vektorok által bezárt belső szög $\beta=96,4^{\circ}$, így a hozzá tartozó $\pi-\beta$ külső szög már figyelembe veszi a vektorok irányítását is. Végül a második rezgés fázisszöge $$\phi_2=\phi_1-(\pi-\beta)=-150^{\circ}+96,4^{\circ}=-53,6^{\circ}$$ Másik megoldás is lehetséges: $$\phi_2=\phi_1+(\pi-\beta)=210^{\circ}-96,4^{\circ}=113,6^{\circ}$$</wlatex> |
</noinclude> | </noinclude> | ||
A lap 2013. június 11., 14:31-kori változata
Feladat
- (*6.21.) Azonos frekvenciájú, egyirányú rezgések összetevésénél az egyik rezgés amplitúdója
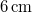 , kedzőfázisa
, kedzőfázisa 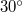 , a másik rezgés amplitúdója
, a másik rezgés amplitúdója 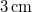 .
.
- a) Mekkorára kell választani a második rezgés kezdőfázisát, hogy az eredő rezgés kezdőfázisa zérus legyen?
- b) Mekkora lesz ebben az esetben az eredő rezgés amplitúdója?
- c) Mekkorára kell a második rezgés kezdőfázisát választani, hogy az eredő amplitúdó
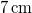 legyen?
legyen?
Megoldás
a) A forgóvektorok vagy a komplex amplitúdók ábrázolásából következik, hogy a második rezgés kezdőfázisa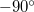 kell legyen.
b) Ugyancsak a kapott derékszögű vektorháromszög alapján
kell legyen.
b) Ugyancsak a kapott derékszögű vektorháromszög alapján 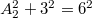 (cm-ekben értve mindent), így
(cm-ekben értve mindent), így ![\[A_2=\sqrt{27}\,\rm{cm}=3\sqrt3\,\rm{cm}\approx5,2\,\rm{cm}\]](/images/math/d/e/4/de4f3ad75357908fb9420686859f04d7.png)
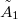 komplex amplitúdó
komplex amplitúdó 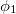 fázisszöge is. Alkalmazva a koszinusz-tételt az
fázisszöge is. Alkalmazva a koszinusz-tételt az 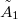 és
és 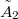 vektorok által bezárt belső szög
vektorok által bezárt belső szög 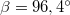 , így a hozzá tartozó
, így a hozzá tartozó 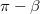 külső szög már figyelembe veszi a vektorok irányítását is. Végül a második rezgés fázisszöge
külső szög már figyelembe veszi a vektorok irányítását is. Végül a második rezgés fázisszöge ![\[\phi_2=\phi_1-(\pi-\beta)=-150^{\circ}+96,4^{\circ}=-53,6^{\circ}\]](/images/math/8/e/e/8ee450350ef46425d428c326554154b9.png)
![\[\phi_2=\phi_1+(\pi-\beta)=210^{\circ}-96,4^{\circ}=113,6^{\circ}\]](/images/math/b/c/9/bc97423b0f947a8331900af170bf1e55.png)
