„Elektrosztatika példák - Összeolvadt felhő-vízcseppek potenciálja” változatai közötti eltérés
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 2. Kategória:Szerkesztő:Beleznai Kategória:Elektrosztatika {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| 39. sor: | 39. sor: | ||
$$E=-\dfrac{\partial U}{\partial z}=-\dfrac{\omega}{2\varepsilon_0}\left( \dfrac{z}{\sqrt{R^2+z^2}}-1\right)$$ | $$E=-\dfrac{\partial U}{\partial z}=-\dfrac{\omega}{2\varepsilon_0}\left( \dfrac{z}{\sqrt{R^2+z^2}}-1\right)$$ | ||
| − | Mely megadja a kérdéses pontban a térerősséget. Ezt vessük össze a | + | Mely megadja a kérdéses pontban a térerősséget. Ezt vessük össze a [[Elektrosztatika példák - Egyenletesen töltött körlap tengelye mentén a potenciáltér|Egyenletesen töltött körlap tengelye mentén a potenciáltér]] megoldásával, ahol ugyanezen geometria elektromos terét kellett meghatározni térerősség vektorok összegzésével: |
$$E=\dfrac{\omega}{2\varepsilon_{0}} \left(1-\dfrac{z}{(R^2+z^2)^{1/2}} \right)$$ | $$E=\dfrac{\omega}{2\varepsilon_{0}} \left(1-\dfrac{z}{(R^2+z^2)^{1/2}} \right)$$ | ||
A lap 2013. június 26., 15:37-kori változata
Feladat
- A felhőkben levő vízcseppeket kis sugarú gömböknek lehet tekinteni, amelyek egymástól olyan távolságban vannak, hogy töltésük a többiektől függetlenül jön létre. Tegyük fel azt, hogy a felhőt alkotó apró vízcseppek átmérője
és átlagosan 
potenciálra töltődnek fel. Ha ezek az apró cseppek 
sugarú cseppekké sűrűsödnek, mekkora lesz a nagy cseppek potenciálja a végtelen távoli ponthoz képest?
Megoldás
Először határozzuk meg a felület töltéssűrűségét:
![\[\omega=\dfrac{Q}{R^2\pi} \]](/images/math/a/9/3/a93035a285903ef4e3fdf8b33caa23dd.png)
Ezt követően parametrizáljuk a körlap felületét és 
polárkoordináták szerint. Válasszunk ki egy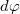 
szög alatt látszódó, a középponttól távolságra levő kicsiny felületdarabot, melynek sugár irányú szélessége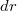 
(1. ábra). Ezen infinitezimális felületelem 
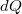töltése:
![\[dQ=\omega rd\varphi dr\]](/images/math/d/1/9/d19301c92d07ed1fe31bee8d355f08bf.png)
Ezen infinitezimális felületelem ponttöltésnek tekinthető, melynek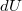 
potenciál járuléka a kérdéses pontban:
![\[dU=\dfrac{1}{4\pi\varepsilon_0}\dfrac{dQ}{t}=\dfrac{1}{4\pi\varepsilon_0}\dfrac{\omega r}{t}d\varphi dr\]](/images/math/d/3/d/d3df6222e49355f1e72c91bf89c54b17.png)
Ahol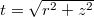 
a felületelem és a kérdéses pont távolsága. Ha a teljes felület által keltett potenciálra vagyunk kíváncsiak, a szuperpozíció elve alapján skalárisan összegeznünk kell az egyes felületelemek 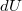potenciál járulékait:
![\[U=\int_0^R \int_0^{2\pi}dU=\dfrac{\omega}{4\pi\varepsilon_0} \int_0^R \int_0^{2\pi} \dfrac{r}{(r^2+z^2)^{1/2}}d\varphi dr\]](/images/math/f/7/9/f79fe701949c1ee30feec24a19c59d15.png)
![\[U=\dfrac{\omega}{4\pi\varepsilon_0} 2\pi\int_0^R \dfrac{r}{(r^2+z^2)^{1/2}} dr=\dfrac{\omega}{2\varepsilon_0}\left( \sqrt{R^2+z^2}-z\right)\]](/images/math/c/e/a/cea2cd1a07384b70521cd7b2fa8bbd74.png)
Behelyettesítve a felületi töltéssűrűségre kapott összefüggést:
![\[U=\dfrac{Q}{2\pi\varepsilon_0 R^2}\left( \sqrt{R^2+z^2}-z\right)\]](/images/math/4/d/c/4dc49776c2a3ca89afc6003435cb5112.png)
Érdekesség:
Érdemes kiszámítani a kapott potenciál negatív gradiensét:
![\[E=-\dfrac{\partial U}{\partial z}=-\dfrac{\omega}{2\varepsilon_0}\left( \dfrac{z}{\sqrt{R^2+z^2}}-1\right)\]](/images/math/9/4/0/9406a334197c49556499cc4db0c441c5.png)
Mely megadja a kérdéses pontban a térerősséget. Ezt vessük össze a Egyenletesen töltött körlap tengelye mentén a potenciáltér megoldásával, ahol ugyanezen geometria elektromos terét kellett meghatározni térerősség vektorok összegzésével:
![\[E=\dfrac{\omega}{2\varepsilon_{0}} \left(1-\dfrac{z}{(R^2+z^2)^{1/2}} \right)\]](/images/math/e/7/6/e760b68831c68f2b1ca6a11b95ddee89.png)
A két számítási módszer megegyező eredménye szívderítő.
