Mechanika - Kiskocsik rugóval
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2013. augusztus 29., 15:20-kor történt szerkesztése után volt.
Feladat
- (*6.16.) Vízszintes lapon álló
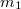 és
és 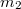 tömegű kiskocsikat
tömegű kiskocsikat  rugóállandójú rugóval kötünk össze. A két kiskocsit széthúzzuk, majd hirtelen elengedjük őket. Hogyan fognak ezután mozogni? (A súrlódástól eltekintünk.)
rugóállandójú rugóval kötünk össze. A két kiskocsit széthúzzuk, majd hirtelen elengedjük őket. Hogyan fognak ezután mozogni? (A súrlódástól eltekintünk.)
Megoldás
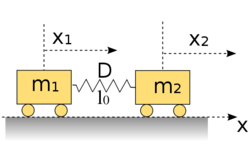
A rajzon látható koordinátarendszerben a két test mozgásegyenlete:![\[m_1\ddot x_1=-D(x_1-x_2)\]](/images/math/5/4/5/54529601f1318a9e2a6175ce3980ecf2.png)
![\[m_2\ddot x_2=D(x_1-x_2),\]](/images/math/2/a/6/2a6be18e9486fc4b65077478c0274ca3.png)
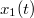 és
és 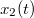 a keresett megoldások. Mivel a testekre pontrendszerként tekintve őket csak belső erő hat (erő-ellenerő pár, ahogy a mozgásegyenletek jobb oldalán látszik), ezért a tömegközéppont mozgása csak meghatározott lehet. A nulla keződsebeségek miatt ennek sebessége nulla (az eredő impulzus nulla). Emiatt a tömegközéppont gyorsulása is nulla, ami a két egyenlet összeadásából is látszik, másrészt a tömegközéppont helye időben állandó. Előbbi megállapítás miatt a két keresett gyorsulás függvény csak egymás számszorosa lehet, mivel másképp nem tudnák kielégíteni a mozgásegyenleteket minden időpontban. Ugyanez igaz a sebesség függvényekre, mivel
a keresett megoldások. Mivel a testekre pontrendszerként tekintve őket csak belső erő hat (erő-ellenerő pár, ahogy a mozgásegyenletek jobb oldalán látszik), ezért a tömegközéppont mozgása csak meghatározott lehet. A nulla keződsebeségek miatt ennek sebessége nulla (az eredő impulzus nulla). Emiatt a tömegközéppont gyorsulása is nulla, ami a két egyenlet összeadásából is látszik, másrészt a tömegközéppont helye időben állandó. Előbbi megállapítás miatt a két keresett gyorsulás függvény csak egymás számszorosa lehet, mivel másképp nem tudnák kielégíteni a mozgásegyenleteket minden időpontban. Ugyanez igaz a sebesség függvényekre, mivel ![\[(m_1+m_2)v_{\rm{TKP}}=0=m_1\dot x_1+m_2\dot x_2,\]](/images/math/5/d/c/5dca4661f392bdd303c455f242df828f.png)
![\[(m_1+m_2)x_{\rm{TKP}}=\text{áll.}=m_1x_1+m_2(l_0+x_2),\]](/images/math/c/8/2/c82ee1c6c13caba47b188e486fba16f0.png)
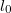 a rugó nyújtatlan hossza, amely viszont nem szerepel a mozgásegyenletekben, így tetszőlegesen választható! Ezzel
a rugó nyújtatlan hossza, amely viszont nem szerepel a mozgásegyenletekben, így tetszőlegesen választható! Ezzel 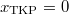 is lehet, és a két keresett függvényre
is lehet, és a két keresett függvényre ![\[\frac{x_1}{x_2}=-\frac{m_2}{m_1}\]](/images/math/f/a/d/fad1df4ca93ba13c8aa23bbc5f033825.png)
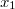 és
és 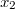 egymással helyettesíthető a két mozgásegyenletben, így kapjuk pl. a másodikból:
egymással helyettesíthető a két mozgásegyenletben, így kapjuk pl. a másodikból: ![\[m_2\ddot x_2=-D(x_2-x_1)=-D\left(x_2+\frac{m_2}{m_1}x_2\right)=-D\frac{m_1+m_2}{m_1}x_2,\]](/images/math/c/d/d/cdd37016d9ce3950664c8d6923e52066.png)
![\[\omega^2=D\frac{m_1+m_2}{m_1m_2},\]](/images/math/2/5/6/2566abb0233b86baee4baea4d1c28e93.png)
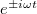 komplex exponenciális vagy szinuszos alakokban kereshetjük a megoldást, mivel rezgésről van szó. Ezek alapján a próbafüggvényeink legyenek
komplex exponenciális vagy szinuszos alakokban kereshetjük a megoldást, mivel rezgésről van szó. Ezek alapján a próbafüggvényeink legyenek 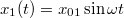 és
és 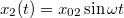 alakúak. Itt már felhasználtuk azt a megállapítást, hogy a két függvény egymás számszorosa lehet csak, tehát azonos frekvenciájú rezgéseket írnak le. Ezeket az egyenletekbe helyettesítve kapjuk
alakúak. Itt már felhasználtuk azt a megállapítást, hogy a két függvény egymás számszorosa lehet csak, tehát azonos frekvenciájú rezgéseket írnak le. Ezeket az egyenletekbe helyettesítve kapjuk ![\[-m_1\omega^2x_1=-D(x_1-x_2)\]](/images/math/b/a/5/ba55e7c43f7cb86a3aa9d4f9fae55efd.png)
![\[-m_2\omega^2x_2=D(x_1-x_2),\]](/images/math/a/8/6/a86b80a6bda082b5ecce07ecc5b2c05d.png)
![\[\begin{bmatrix} D-m_1\omega^2&-D\\-D&D-m_2\omega^2 \end{bmatrix} \begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}\]](/images/math/d/d/5/dd5342bdfbb2652bbdefd856be49554b.png)
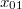 és
és 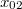 amplitúdók alkotta vektor lenne a sajátvektor. Konkrét kezdeti feltételek nélkül ezek nem határozatók meg, csak az arányuk, azaz egy sajátvektor, amely a nem nulla frekvenciás rezgéshez tartozik. Hasonló lineáris algebrai eszköztárral kezelhetők akár a több szabadsági fokú rugóláncok, csatolt ingák, stb.
amplitúdók alkotta vektor lenne a sajátvektor. Konkrét kezdeti feltételek nélkül ezek nem határozatók meg, csak az arányuk, azaz egy sajátvektor, amely a nem nulla frekvenciás rezgéshez tartozik. Hasonló lineáris algebrai eszköztárral kezelhetők akár a több szabadsági fokú rugóláncok, csatolt ingák, stb.