Mechanika - Rezgés ferde rugóval
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen BernathB (vitalap | szerkesztései) 2013. június 20., 13:45-kor történt szerkesztése után volt.
Feladat
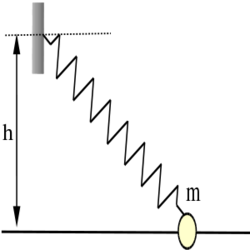
- (*6.14.) Az ábrán látható
 tömegű test a vízszintes rúdon súrlódás nélkül mozoghat. A hozzá kapcsolódó rugó másik végpontját a rúdtól
tömegű test a vízszintes rúdon súrlódás nélkül mozoghat. A hozzá kapcsolódó rugó másik végpontját a rúdtól  távolságra rögzítjük. A rugó nyugalmi hossza
távolságra rögzítjük. A rugó nyugalmi hossza 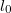 , rugóállandója
, rugóállandója  . Határozzuk meg az egyensúlyi helyzet körüli kis rezgések frekvenciáját különböző
. Határozzuk meg az egyensúlyi helyzet körüli kis rezgések frekvenciáját különböző  távolságok esetén! Vizsgáljuk meg a
távolságok esetén! Vizsgáljuk meg a 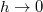 és
és 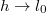 határeseteket! ÁBRA
határeseteket! ÁBRA
Megoldás
A 6.9. feladathoz hasonlóan meg lehet határozni egy effektív rugóállandót. A rugó nyújtatlan állapotában a test legyen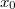 távolságra a rúd kiszemelt pontjától:
távolságra a rúd kiszemelt pontjától: ![\[h^2+x_0^2=l_0^2\]](/images/math/b/f/9/bf908606ba8c222d229332e4a50d7907.png)
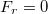 . Ebből
. Ebből 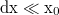 mértékben kimozdítva a rugó hossza
mértékben kimozdítva a rugó hossza  -re változik, melyre
-re változik, melyre 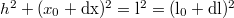 . Keressük a rugó
. Keressük a rugó 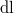 kis hosszváltozását
kis hosszváltozását 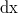 -ben elsőrendű közelítésben. Az előbbi Pitagorasz-tételben a zárójeleket bontva a másodrendben kicsi tagokat elhagyva kapjuk:
-ben elsőrendű közelítésben. Az előbbi Pitagorasz-tételben a zárójeleket bontva a másodrendben kicsi tagokat elhagyva kapjuk: 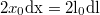 , azaz
, azaz ![\[\rm dl=\frac{x_0}{l_0}\rm dx=\cos{\alpha}\rm dx,\]](/images/math/0/d/4/0d48222507ebbe823e38759efa119d59.png)
 a rugó és a rúd által bezárt szög. Ez utóbbi összefüggést egy megfelelő ábrából is leolvashattuk volna. Ezzel a rugóerő kis kitérésekre közelített alakja
a rugó és a rúd által bezárt szög. Ez utóbbi összefüggést egy megfelelő ábrából is leolvashattuk volna. Ezzel a rugóerő kis kitérésekre közelített alakja ![\[F_r=-D\rm dl=-D\frac{x_0}{l_0}\rm dx,\]](/images/math/1/9/f/19f208780529b81f576a4b7ec158a6fc.png)
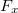 komponense az egyedüli erő abban az irányban, tehát a mozgásegyenlet
komponense az egyedüli erő abban az irányban, tehát a mozgásegyenlet ![\[m\ddot x=F_x=F_r\cos{\alpha}=F_r\frac{x_0}{l_0}=-D\frac{x_0^2}{l_0^2}\rm dx=-D\frac{l_0^2-h^2}{l_0^2}\rm dx,\]](/images/math/2/7/b/27bd9acb251899e0da483fe70ad401f9.png)
![\[D_{\rm{eff}}=D\frac{l_0^2-h^2}{l_0^2}\]](/images/math/8/4/6/8467532d3b36d59fa08462e3d0a3dfa6.png)
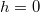 esetén visszaadja
esetén visszaadja  -t,
-t, 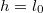 esetén pedig nulla, azaz nem alakul ki harmonikus rezgés kis kitéréseknél.
esetén pedig nulla, azaz nem alakul ki harmonikus rezgés kis kitéréseknél.