Elektrosztatika példák - Végtelen hosszú egyenes fonálpár elektromos tere
Feladat
- Egymástól
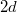 távolságban párhuzamosan elhelyezett két igen hosszú fonalat egyenletesen töltünk fel
távolságban párhuzamosan elhelyezett két igen hosszú fonalat egyenletesen töltünk fel 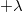 és
és 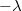 lineáris töltéssűrűséggel. Határozzuk meg a térerősséget abban a pontban, mely a két fonalat magában foglaló síktól
lineáris töltéssűrűséggel. Határozzuk meg a térerősséget abban a pontban, mely a két fonalat magában foglaló síktól  távolságban helyezkedik el a rendszer szimmetriasíkjában!
távolságban helyezkedik el a rendszer szimmetriasíkjában!
Megoldás
Először határozzuk meg a 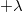 töltéssűrűségű fonal terét a fonaltól mért
töltéssűrűségű fonal terét a fonaltól mért  távolságban. (A másik fonaltól egyelőre tekintsünk el) Ehhez felveszünk egy
távolságban. (A másik fonaltól egyelőre tekintsünk el) Ehhez felveszünk egy  sugarú hengerfelületet, melynek tengelye egybeesik a vonaltöltéssel, magassága
sugarú hengerfelületet, melynek tengelye egybeesik a vonaltöltéssel, magassága  . A hengerfelületre felírjuk a Gauss-törvényt:
. A hengerfelületre felírjuk a Gauss-törvényt:
![\[\dfrac{Q}{\varepsilon_0}=\oint \overline{E}\overline{dA} \]](/images/math/b/0/1/b01a772d8bb04564543763751783eb58.png)
Ahol 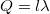 a hengerfelület által bezárt töltés mennyisége. A rendszer szimmetriája miatt feltételezhetjük, hogy a térerősség radiális eloszlású, és a tér minden pontjában merőleges a vonaltöltésre. Megállapíthatjuk, hogy a hengerek alapjain a felület
a hengerfelület által bezárt töltés mennyisége. A rendszer szimmetriája miatt feltételezhetjük, hogy a térerősség radiális eloszlású, és a tér minden pontjában merőleges a vonaltöltésre. Megállapíthatjuk, hogy a hengerek alapjain a felület 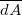 normálisa mindenütt
normálisa mindenütt 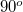 -ot zár be a feltételezett
-ot zár be a feltételezett 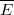 térerősséggel. Tehát a
térerősséggel. Tehát a 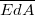 skalárszorzat a henger alapjainak minden pontján nullának tekinthető.
A henger palástján a térerősség minden pontban párhuzamos a felületnormálissal,így a skalárszorzat megegyezik a vektorok nagyságának szorzatával:
skalárszorzat a henger alapjainak minden pontján nullának tekinthető.
A henger palástján a térerősség minden pontban párhuzamos a felületnormálissal,így a skalárszorzat megegyezik a vektorok nagyságának szorzatával: 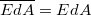 A térerősség zárt felületre vett integrálja tehát egyszerűen kifejezhető:
A térerősség zárt felületre vett integrálja tehát egyszerűen kifejezhető:
![\[\dfrac{l\lambda}{\varepsilon_0}=\oint \overline{E}\overline{dA}=2r\pi lE \]](/images/math/5/3/b/53b1b48e05a604f15c0421a8306932a4.png)
Ahol 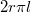 a henger palástjának területe. A térerősség az egyenletből kifejezhető:
a henger palástjának területe. A térerősség az egyenletből kifejezhető:
![\[ E=\dfrac{\lambda}{2\pi\varepsilon_0}\dfrac{1}{r}\]](/images/math/a/f/c/afcfd06885e5639c9546c927faaeb1e9.png)
A feladatban két vonaltöltés terét kell meghatározni egy adott pontban. A kérdéses pont a vonaltöltésektől egyaránt  távolságban található, ahol:
távolságban található, ahol:
![\[r=\sqrt{d^2+z^2}\]](/images/math/d/7/c/d7c8bb5a0b13aabc1e7e4213d62613f0.png)
A töltéssűrűségek abszolút értéke is megegyezik, így az egyes vonaltöltések által az adott pontban keltett elektromos tér 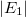 és
és 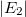 járulékainak abszolút értéke is megegyezik. A járulékok összegzése a szuperpozíció elve alapján történik. Az eredő tér tehát párhuzamos a két vonaltöltés által kijelölt síkkal, a vonaltöltésekre pedig merőleges. Nagysága a következőképp számítható:
járulékainak abszolút értéke is megegyezik. A járulékok összegzése a szuperpozíció elve alapján történik. Az eredő tér tehát párhuzamos a két vonaltöltés által kijelölt síkkal, a vonaltöltésekre pedig merőleges. Nagysága a következőképp számítható:
![\[ E_e=2\dfrac{\lambda}{2\pi\varepsilon_0}\dfrac{1}{\sqrt{d^2+z^2}}cos\Theta\]](/images/math/6/8/c/68c8e876f6acb5c2fb882c18c8208ad7.png)
Ahol 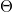 az
az  és a két vonaltöltés síkja által bezárt szög. Ez alapján felírható, hogy:
és a két vonaltöltés síkja által bezárt szög. Ez alapján felírható, hogy:
![\[cos\Theta=\dfrac{d}{r}=\dfrac{d}{\sqrt{d^2+z^2}} \]](/images/math/c/6/c/c6c746a628e652e7cf72fa1b18c5d19e.png)
A térerősség a kérdéses pontban tehát:
![\[ E_e=\dfrac{\lambda}{\pi\varepsilon_0}\dfrac{d}{(d^2+z^2)}\]](/images/math/9/c/0/9c0c16af5ed3b4ee67e6c1206b32a413.png)