| [rejt] Navigáció Pt·1·2·3
|
| Kísérleti fizika gyakorlat 2.
|
Gyakorlatok listája:
- Erőhatások elektromos erőtérben, elektromos térerősség
- Elektromos potenciál
- Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok
- Kapacitás, kondenzátorok. Elrendezések energiája
- Vezetőképesség, áramsűrűség
- Biot-Savart törvény, gerjesztési törvény
- Erőhatások mágneses térben
- Mágneses térerősség. Kölcsönös és öninduktivitás
- Az indukció törvénye, mozgási indukció
- Mágneses tér energiája. Váltakozó áram, eltolási áram
|
| Elektrosztatika - Erőhatások elektromos erőtérben, elektromos térerősség
|
Feladatok listája:
- Négyszög sarkaiba helyezett ponttöltések elektromos tere
- Két töltést összekötő egyenes mentén az elektromos tér
- Körvezető tengelye mentén az elektromos tér
- Egyenletesen töltött körlap tengelye mentén az elektromos tér
- Végtelen hosszú egyenes fonál elektromos tere 1.
- Végtelen hosszú egyenes fonál elektromos tere 2.
- Végtelen sík elektromos tere
- Két, egymásra merőleges végtelen sík elektromos tere
- Homogén térfogati töltéssűrűségű töltött gömb elektromos tere
- Földelt gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
- Egyenletesen töltött gömbben lévő, gömb alakú üreg elektromos tere
- Végtelen hosszú egyenes fonálpár elektromos tere
- Az elektromos térerősség helyfüggő lineáris töltéssűrűségű szigetelő gyűrű tengelye mentén
- Vezető gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064
|
Feladat
- Egy
 oldalú négyzet csúcspontjaiba egyforma
oldalú négyzet csúcspontjaiba egyforma 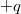 töltést helyezünk.Mekkora és milyen irányú erő hat egy-egy töltésre? Hova kellene helyezni egy újabb töltést, hogy egyikre se hasson erő? Mekkora nagyságú, és milyen előjelű ez a töltés?
töltést helyezünk.Mekkora és milyen irányú erő hat egy-egy töltésre? Hova kellene helyezni egy újabb töltést, hogy egyikre se hasson erő? Mekkora nagyságú, és milyen előjelű ez a töltés?
Megoldás
Ha a kiszemelt töltésen az ábrán látható módon felveszünk egy koordináta rendszert, akkor annak helyén a többi töltés által keltett térerősség:
Ahol 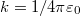 . A
. A 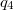 töltésrere ható elektromos tér a három töltés szuperpozíciójaként áll elő. Látható, hogy a négyzet átlójára merőleges erők éppen kiejtik egymást, így a kiszemelt töltésre csak átló irányú tér fog hatni. Ennek nagysága pedig:
töltésrere ható elektromos tér a három töltés szuperpozíciójaként áll elő. Látható, hogy a négyzet átlójára merőleges erők éppen kiejtik egymást, így a kiszemelt töltésre csak átló irányú tér fog hatni. Ennek nagysága pedig:
Amiből a töltésre ható erő:
Ha azt szeretnénk, hogy egyik töltésre se hasson erő, akkor pedig a négyzet középpontjába kell egy olyan 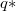 ellentétes előjelű töltést tennünk, amely által keltett erő éppen ellenttart a négyzet többi töltése által okozott eredő erővel.
ellentétes előjelű töltést tennünk, amely által keltett erő éppen ellenttart a négyzet többi töltése által okozott eredő erővel.
Innen pedig:
 oldalú négyzet csúcspontjaiba egyforma
oldalú négyzet csúcspontjaiba egyforma 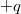 töltést helyezünk.Mekkora és milyen irányú erő hat egy-egy töltésre? Hova kellene helyezni egy újabb töltést, hogy egyikre se hasson erő? Mekkora nagyságú, és milyen előjelű ez a töltés?
töltést helyezünk.Mekkora és milyen irányú erő hat egy-egy töltésre? Hova kellene helyezni egy újabb töltést, hogy egyikre se hasson erő? Mekkora nagyságú, és milyen előjelű ez a töltés?
![\[\vec{E_{2}} = \frac{k\cdot{q}}{(a\cdot{\sqrt{2}})^2}\cdot\vec{e_{x}} \]](/images/math/7/d/8/7d8770394c6257771022629369fde369.png)
![\[\vec{E_{1}} = \frac{k\cdot{q}}{{a}^2}\cdot\vec{e_{x}}\cdot{\cos(\alpha)}+ \frac{k\cdot{q}}{{a}^2}\cdot\vec{e_{y}}\cdot{\sin(\alpha)} \]](/images/math/c/5/8/c5849a0651495cea680a6084f038305e.png)
![\[\vec{E_{3}} = \frac{k\cdot{q}}{{a}^2}\cdot\vec{e_{x}}\cdot{\cos(\alpha)}- \frac{k\cdot{q}}{{a}^2}\cdot\vec{e_{y}}\cdot{\sin(\alpha)} \]](/images/math/3/5/2/3523667ed2fcc2a95bb620b93f22b1d8.png)
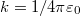 . A
. A 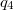 töltésrere ható elektromos tér a három töltés szuperpozíciójaként áll elő. Látható, hogy a négyzet átlójára merőleges erők éppen kiejtik egymást, így a kiszemelt töltésre csak átló irányú tér fog hatni. Ennek nagysága pedig:
töltésrere ható elektromos tér a három töltés szuperpozíciójaként áll elő. Látható, hogy a négyzet átlójára merőleges erők éppen kiejtik egymást, így a kiszemelt töltésre csak átló irányú tér fog hatni. Ennek nagysága pedig:
![\[\vec{E_{e}}=\frac{k\cdot{q}}{a^{2}}\cdot{(\frac{1}{2}+\sqrt{2})}\cdot{\vec{e_{x}}}\]](/images/math/5/2/2/52287ab3eb24deddd6be4b8440501b46.png)
![\[\vec{F}=\frac{k\cdot{q^{2}}}{a^{2}}\cdot{(\frac{1}{2}+\sqrt{2})}\cdot{\vec{e_{x}}}\]](/images/math/6/9/2/6924db8f74613762e896dc333f5f8e09.png)
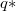 ellentétes előjelű töltést tennünk, amely által keltett erő éppen ellenttart a négyzet többi töltése által okozott eredő erővel.
ellentétes előjelű töltést tennünk, amely által keltett erő éppen ellenttart a négyzet többi töltése által okozott eredő erővel.
![\[\vec{F*}=\vec{-F_{e}} \]](/images/math/8/4/b/84b27c911e8470a954434ae70aa07f3b.png)
![\[\frac{k\cdot{q^2}}{a^2}\cdot{(\frac{1}{2}+\sqrt{2})}=-\frac{k\cdot{q}\cdot{q*}}{{(\frac{\sqrt{2}}{2}\cdot{a})}^2} \]](/images/math/b/5/1/b5136030dbb9c100eadb2942588420ca.png)
![\[q* = -(\frac{1}{4}+\frac{\sqrt{2}}{2}).\]](/images/math/d/9/1/d9105ea91b5f1e07347113c6dcb80225.png)