| Navigáció Pt·1·2·3
|
| Kísérleti fizika gyakorlat 2.
|
Gyakorlatok listája:
- Erőhatások elektromos erőtérben, elektromos térerősség
- Elektromos potenciál
- Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok
- Kapacitás, kondenzátorok. Elrendezések energiája
- Vezetőképesség, áramsűrűség
- Biot-Savart törvény, gerjesztési törvény
- Erőhatások mágneses térben
- Mágneses térerősség. Kölcsönös és öninduktivitás
- Az indukció törvénye, mozgási indukció
- Mágneses tér energiája. Váltakozó áram, eltolási áram
|
| Elektrosztatika - Erőhatások elektromos erőtérben, elektromos térerősség
|
Feladatok listája:
- Négyszög sarkaiba helyezett ponttöltések elektromos tere
- Két töltést összekötő egyenes mentén az elektromos tér
- Körvezető tengelye mentén az elektromos tér
- Egyenletesen töltött körlap tengelye mentén az elektromos tér
- Végtelen hosszú egyenes fonál elektromos tere 1.
- Végtelen hosszú egyenes fonál elektromos tere 2.
- Végtelen sík elektromos tere
- Két, egymásra merőleges végtelen sík elektromos tere
- Homogén térfogati töltéssűrűségű töltött gömb elektromos tere
- Földelt gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
- Egyenletesen töltött gömbben lévő, gömb alakú üreg elektromos tere
- Végtelen hosszú egyenes fonálpár elektromos tere
- Az elektromos térerősség helyfüggő lineáris töltéssűrűségű szigetelő gyűrű tengelye mentén
- Vezető gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064
|
Feladat
- Egy
 sugarú vékony körvezető töltése
sugarú vékony körvezető töltése  . Határozzuk meg a térerősséget a körvezető tengelyén, a körvezető síkjától
. Határozzuk meg a térerősséget a körvezető tengelyén, a körvezető síkjától  távolságban. A tengely mely pontján a legnagyobb a térerősség?
távolságban. A tengely mely pontján a legnagyobb a térerősség?
Megoldás
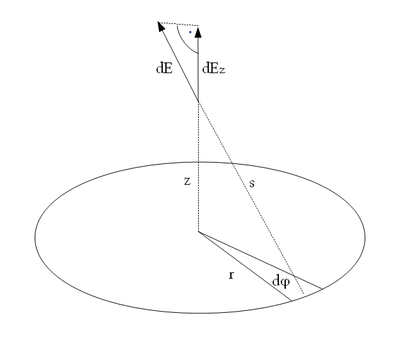
A gyűrűt elemi részekre osztjuk, és a kérdéses pontban összegezzük a gyűrűelemek térerősség járulékait. A gyűrűt az ábrán látható  szög szerint parametrizáljuk, a kört
szög szerint parametrizáljuk, a kört 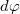 szög alatt látszó ívelemekre bontjuk. Ebben az esetben egy ívelem
szög alatt látszó ívelemekre bontjuk. Ebben az esetben egy ívelem 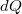 töltése a következő:
töltése a következő:
Az ívelem és a kérdéses pont  távolsága:
távolsága:
A kérdéses pontban Coulomb törvényével meghatározhatjuk az elemi ívdarab 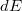 térerősség járulékát:
térerősség járulékát:
A rendszer hengerszimmetriája miatt a 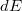 térerősség járulékok szimmetriatengelyre merőleges komponensei kioltják egymást, míg a
térerősség járulékok szimmetriatengelyre merőleges komponensei kioltják egymást, míg a  irányú komponensek összegződnek. A
irányú komponensek összegződnek. A 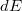 térerősség függőleges komponense:\
térerősség függőleges komponense:\
Ahol  a
a  tengely és
tengely és  által bezárt szög:
által bezárt szög:
Összegezzük az elemi ívdarabok  irányú térerősség járulékát, és megkapjuk a térerősség értékét a kérdéses pontban:
irányú térerősség járulékát, és megkapjuk a térerősség értékét a kérdéses pontban:
Ezt követően határozzuk meg a maximális térerősség  helyét! A szélsőértéket az alábbi egyenlet megoldásával kereshetjük meg:
helyét! A szélsőértéket az alábbi egyenlet megoldásával kereshetjük meg:
Az  térerősség
térerősség  szerinti deriváltja:
szerinti deriváltja:
A megoldandó egyenlet tehát:
A megoldás:
 sugarú vékony körvezető töltése
sugarú vékony körvezető töltése  . Határozzuk meg a térerősséget a körvezető tengelyén, a körvezető síkjától
. Határozzuk meg a térerősséget a körvezető tengelyén, a körvezető síkjától  távolságban. A tengely mely pontján a legnagyobb a térerősség?
távolságban. A tengely mely pontján a legnagyobb a térerősség?
 szög szerint parametrizáljuk, a kört
szög szerint parametrizáljuk, a kört 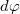 szög alatt látszó ívelemekre bontjuk. Ebben az esetben egy ívelem
szög alatt látszó ívelemekre bontjuk. Ebben az esetben egy ívelem 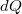 töltése a következő:
töltése a következő:
![\[dQ=\dfrac{d\varphi}{2\pi}Q\]](/images/math/5/d/6/5d615f04feb68c17e29607b7d89bd1a6.png)
 távolsága:
távolsága:
![\[s=\sqrt{r^2+z^2}\]](/images/math/b/3/2/b328e13bb715895af840b4a7e80c9295.png)
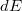 térerősség járulékát:
térerősség járulékát:
![\[dE=\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{dQ}{s^2}=\dfrac{1}{4\pi\varepsilon_{0}}\dfrac{\dfrac{d\varphi}{2\pi}Q}{r^2+z^2} \]](/images/math/5/a/2/5a29c87a586a5d0ef86b11016abc9354.png)
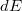 térerősség járulékok szimmetriatengelyre merőleges komponensei kioltják egymást, míg a
térerősség járulékok szimmetriatengelyre merőleges komponensei kioltják egymást, míg a  irányú komponensek összegződnek. A
irányú komponensek összegződnek. A 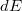 térerősség függőleges komponense:\
térerősség függőleges komponense:\
![\[dE_{z}=dEcos(\theta)\]](/images/math/a/7/6/a7683ce2b0138eeb57c5ec6dda08c86c.png)
 a
a  tengely és
tengely és  által bezárt szög:
által bezárt szög:
![\[cos(\theta)=\dfrac{z}{\sqrt{r^2+z^2}}\]](/images/math/c/3/6/c3625baa5a9b9a4e5ccd37db5d8ffe3b.png)
![\[dE_{z}=\dfrac{Q}{4\pi\varepsilon_{0}}\dfrac{d\varphi}{2\pi}\dfrac{z}{(r^2+z^2)^{3/2}}\]](/images/math/6/4/e/64ee7398b38494d56d91b7cdb37c0ff1.png)
 irányú térerősség járulékát, és megkapjuk a térerősség értékét a kérdéses pontban:
irányú térerősség járulékát, és megkapjuk a térerősség értékét a kérdéses pontban:
![\[ E=\int_0^{2\pi}dE_z=\dfrac{Q}{4\pi\varepsilon_{0}}\dfrac{z}{2\pi(r^2+z^2)^{3/2}}\int_0^{2\pi}d\varphi=\dfrac{Q}{4\pi\varepsilon_{0}}\dfrac{z}{(r^2+z^2)^{3/2}} \]](/images/math/f/d/7/fd71fbdcb2fdaf9d0152e4cc6cbe358f.png)
 helyét! A szélsőértéket az alábbi egyenlet megoldásával kereshetjük meg:
helyét! A szélsőértéket az alábbi egyenlet megoldásával kereshetjük meg:
![\[ \dfrac{dE}{dz}=0\]](/images/math/d/8/6/d86f4b57bb727edb91c93dd1a861468f.png)
 térerősség
térerősség  szerinti deriváltja:
szerinti deriváltja:
![\[ \frac{dE}{dz}=\frac{(r^2+z^2)^{3/2}-3z^2(r^2+z^2)^{1/2}}{(r^2+z^2)^3}\]](/images/math/2/a/e/2ae1a4ed7ce9493c0d84f0058e030ee0.png)
![\[ 0=(r^2+z^2)^{3/2}-3z^2(r^2+z^2)^{1/2}\]](/images/math/0/5/2/05230a426e33001f98ad8251a8ef4875.png)
![\[ z=\dfrac{r}{\sqrt{2}}\]](/images/math/8/2/5/82567e131eb8f6e89cf20bf7109cac64.png)