Elektrosztatika példák - Vezető gömbhéjjal koncentrikusan körülvett egyenletesen töltött gömb elektromos tere

Feladat

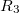1. $\setbox0\hbox{$R_1$}% \message{//depth:\the\dp0//}% \box0%$ sugarú szigetelő gömb térfogatában $\setbox0\hbox{$Q$}% \message{//depth:\the\dp0//}% \box0%$ töltés oszlik el egyenletesen. A gömböt egy véges vastagságú fém gömbhéj veszi körül, melynek görbületi sugarai $\setbox0\hbox{$R_2$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$R_3$}% \message{//depth:\the\dp0//}% \box0%$. A gömbhéj eredő töltése 0.
   a) Határozzuk meg a szigetelő gömbben a térfogati töltéssűrűséget!
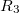   b) Milyen előjelű és milyen nagyságú felületi töltéssűrűség alakul ki az $\setbox0\hbox{$R_2$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$R_3$}% \message{//depth:\the\dp0//}% \box0%$ sugarú felületeken?
   c) Határozzuk meg a térerősséget az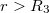 $\setbox0\hbox{$r>R_3$}% \message{//depth:\the\dp0//}% \box0%$ sugáron!
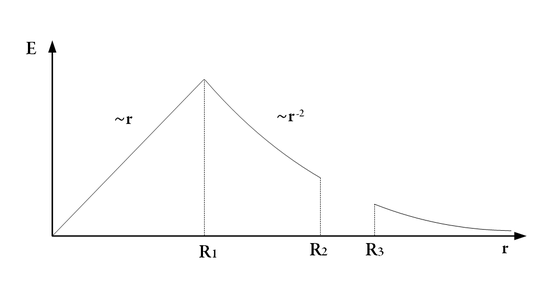
   d) Rajzoljuk fel jellegre helyesen az elektromos térerősséget, mint a távolság függvényét!

Megoldás

a)

A gömb térfogati töltéssűrűsége:

$\[\varrho=\dfrac{Q}{\dfrac{4}{3}R_1^3\pi}\]$

b)

A fémfelületen töltésmegosztás jön létre úgy, hogy a fém belsejében a tér nulla lesz, továbbá a fém gömbhéj össztöltése szintén nulla marad. Hogy ez megvalósuljon, a gömbhéj belső, $\setbox0\hbox{$R_2$}% \message{//depth:\the\dp0//}% \box0%$ sugarú felületén 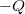$\setbox0\hbox{$-Q$}% \message{//depth:\the\dp0//}% \box0%$, míg a külső, 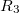$\setbox0\hbox{$R_3$}% \message{//depth:\the\dp0//}% \box0%$ sugarú felületén $\setbox0\hbox{$Q$}% \message{//depth:\the\dp0//}% \box0%$ töltés halmozódik fel. A felületi töltéssűrűségek tehát egyszerűen kiszámíthatóak:

$\[\omega_2=\dfrac{-Q}{4R_2^2\pi}\]$

illetve:

$\[\omega_3=\dfrac{Q}{4R_3^2\pi}\]$

c)

A fém gömbhéjon kívül a térerősséget nem befolyásolja a gömbhéj. Ez a Gauss-törvénnyel egyszerűen belátható. Tehát a térerősség meghatározható úgy, mintha csak a $\setbox0\hbox{$Q$}% \message{//depth:\the\dp0//}% \box0%$ töltésű gömb terét kellene kiszámolnunk $\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%$ távolságban:

$\[E=\dfrac{1}{4\pi\varepsilon_0}\dfrac{Q}{r^2}\]$

d)