Mechanika - Rezgő lemezen tapadás

Feladat

1. (6.10.) Síklemez a rajta nyugvó testtel együtt harmonikus rezgést végez a vízszintes síkban. A rezgés amplitúdója 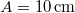$\setbox0\hbox{$A=10\,\rm{cm}$}% \message{//depth:\the\dp0//}% \box0%$. Mekkora a lemez és a test közötti súrlódási együttható, ha a test akkor kezd csúszni a lemezen, amikor a rezgésidő kisebb lesz, mint $\setbox0\hbox{$T=1\,\rm{s}$}% \message{//depth:\the\dp0//}% \box0%$?

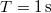Megoldás

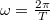Ha a rezgésidő $\setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0%$, a rezgés körfrekvenciája $\setbox0\hbox{$\omega=\frac{2\pi}T$}% \message{//depth:\the\dp0//}% \box0%$, és a test legnagyobb gyorulása 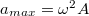$\setbox0\hbox{$a_{max}=\omega^2A$}% \message{//depth:\the\dp0//}% \box0%$. Mivel a testre vízszintesen csak a súrlódási erő hat, a test mozgásegyenlete 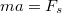$\setbox0\hbox{$ma=F_s$}% \message{//depth:\the\dp0//}% \box0%$. A kritikus pillanat az, amikor a gyorulás a legnagyobb, ekkor a súrlódási erő nem lehet nagyobb a tapadási maximumnál, azaz

$\[ma_{max}=mA\omega^2=F_{s,max}=\mu mg,\]$

mivel a nyomóerő ebben az esetben a nehézségi erővel egyezik meg. Ebből rendezés után

$\[\mu=\frac{A4\pi^2}{gT^2}=0,402\]$