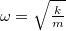Mechanika - Rugóra akasztott test
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. november 29., 16:49-kor történt szerkesztése után volt.
Feladat
- (2.1.24.)
 tömegű testet
tömegű testet  rugóállandójú súlytalan rugóra akasztunk. A testet kezdősebesség nélkül elengedjük abban a helyzetben, amelyben a rugó feszültségmentes. Adjuk meg a kitérést az idő függvényében!
rugóállandójú súlytalan rugóra akasztunk. A testet kezdősebesség nélkül elengedjük abban a helyzetben, amelyben a rugó feszültségmentes. Adjuk meg a kitérést az idő függvényében!
Megoldás
A mozgásegyenlet a nyújtatlan rugó esetén fenálló helyzettől mért koordinátában:![\[m\ddot x=mg-kx\]](/images/math/9/5/8/958e217894685a755d106624941d33f4.png)
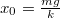 . Mivel a test
. Mivel a test 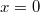 -ból indul és kezdősebesség nélkül,
-ból indul és kezdősebesség nélkül, 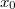 egyben az amplitúdó is. A rezgés
egyben az amplitúdó is. A rezgés 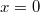 és
és 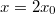 határok között megy végbe. A kitérés-idő függvényt
határok között megy végbe. A kitérés-idő függvényt 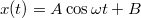 alakban keresve a megadott feltételekhez illeszkedő megoldás
alakban keresve a megadott feltételekhez illeszkedő megoldás ![\[x(t)=\frac{mg}k(1-\cos(\omega t)),\]](/images/math/a/e/7/ae7a20c5010ff2d902b5fdf074d52dbc.png)