Mechanika - Kosárba ejtett test
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. december 2., 14:47-kor történt szerkesztése után volt.
Feladat
- (6.6.) Egy
 tömegű kosár
tömegű kosár  direkciós erejű rugón nyugszik. A kosár felett
direkciós erejű rugón nyugszik. A kosár felett  magasságból
magasságból  tömegű testet ejtünk le, amely rugalmatlanul ütközve a kosárban marad. Milyen amplitúdóval fog rezegni a kosár?
tömegű testet ejtünk le, amely rugalmatlanul ütközve a kosárban marad. Milyen amplitúdóval fog rezegni a kosár?
Megoldás
Az ütközés előtt az egyensúlyi helyzet (ahol a gyorsulás nulla) a rugó nyújtatlan hosszától mérve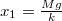 , mely az ütközés után
, mely az ütközés után 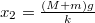 -re módosul, azaz az ütközés utáni pillanatban a kezdeti kitérés
-re módosul, azaz az ütközés utáni pillanatban a kezdeti kitérés ![\[x_2-x_1=\frac{mg}k\]](/images/math/d/8/6/d864f881101065dd28bc738866e610cf.png)
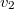 sebeséget is. Ehhez az ejtés közbeni energiamegaradást és a tökéletesen rugalmatlan ütközés impulzusmegmaradását kell felírni:
sebeséget is. Ehhez az ejtés közbeni energiamegaradást és a tökéletesen rugalmatlan ütközés impulzusmegmaradását kell felírni: ![\[\frac12mv^2=mgh\]](/images/math/2/4/4/24489683ed236338c98cfd738376d115.png)
![\[mv=(m+M)v_2\]](/images/math/9/c/5/9c5e6ee7e76421972365218fde81906d.png)
![\[\frac12(m+M)v_2^2+\frac12k(x_2-x_1)^2=\frac12kA^2,\]](/images/math/8/e/3/8e3dddb9d2261410822bf4f7b1051908.png)
![\[A^2=\frac{m^2g^2}{k^2}\left(1+\frac{2kh}{g(m+M)}\right).\]](/images/math/c/2/b/c2bb1eb4c848af069020f7fa3a40a229.png)