Elektrosztatika példák - Koaxilális hengerfelületek potenciáltere
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Beleznai (vitalap | szerkesztései) 2013. április 28., 18:05-kor történt szerkesztése után volt.
Feladat
- Két végtelen hosszú koaxiális hengert egynemű töltéssel töltünk fel úgy, hogy a töltéssűrűség a külső hengeren
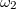 , a belsőn pedig
, a belsőn pedig 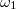 . A hengerek sugara
. A hengerek sugara 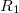 és
és 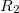 . Határozzuk meg a hengerek közötti potenciálkülönbséget?
. Határozzuk meg a hengerek közötti potenciálkülönbséget?
Megoldás
Vegyünk egy igen hosszú ( 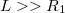 )
)  sugarú hengert, amely körbe zárja a belső hengert, de sugara kisebb a külső henger sugránál. (
sugarú hengert, amely körbe zárja a belső hengert, de sugara kisebb a külső henger sugránál. (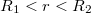 ) Írjuk fel erre a Gauss-tételt:
) Írjuk fel erre a Gauss-tételt:
![\[\vec{E}\cdot 2\cdot r\cdot\pi\cdot L = \frac{\omega_{2}}{\epsilon_{0}}\cdot 2\cdot R_{1}\cdot\pi\cdot L\]](/images/math/e/8/b/e8b93a36408600f6dc7a1b7146a38165.png)
Amiből:
![\[\vec{E}= \frac{\omega_{2}\cdot R_{1}}{\epsilon_{0}\cdot r}\]](/images/math/e/2/e/e2e5f1ff5ce28dc53b7edc79118185d8.png)
A pontenciálkülönbség pedig:
![\[\Delta U = \int_{R_{1}}^{R_{2}}\frac{\omega_{2}\cdot R_{1}}{\epsilon_{0}\cdot r}\cdot dr =\frac{\omega_{2}\cdot R_{1}}{\epsilon_{0}}\cdot \ln\left(\frac{R_{2}}{R_{1}}\right) \]](/images/math/a/3/2/a32796d7e4e70e997416c251e424b512.png)