„Elektrosztatika példák - Egyenletesen töltött gömbtérfogat árnyékolással elektromos tere” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
|||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex>#Egy $R_{1}$ sugarú gömben egyenletes $\rho$ térfogati töltéssűrűség van. Ezt egy $R_{2}$ sugarú földelt fémgömb veszi körül koncentrikus elrendezésben.<br>'''a)''' Határozzuk meg, a térerősséget a gömb középpontjától mért távolság függvényében, a gömbön belül és kívül!<br>'''b)''' Mekkora felületi töltéssűrűség alakul ki a földelt | + | </noinclude><wlatex>#Egy $R_{1}$ sugarú gömben egyenletes $\rho$ térfogati töltéssűrűség van. Ezt egy $R_{2}$ sugarú földelt fémgömb veszi körül koncentrikus elrendezésben.<br>'''a)''' Határozzuk meg, a térerősséget a gömb középpontjától mért távolság függvényében, a gömbön belül és kívül!<br>'''b)''' Mekkora felületi töltéssűrűség alakul ki a földelt gömbhéj belső felületén?</wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk a Gauss tételt a különböző térrészekre!}} {{Végeredmény|content=Ha $r<R_{1}$:$$\vec{E}=\frac{\rho\cdot r}{\epsilon_{0}\cdot 3}\cdot\vec{e_{r}}$$ Ha $R_{1}<r<R_{2}$:: $$\vec{E}=\frac{\rho\cdot R^{3}}{\epsilon_{0}\cdot 3\cdot r^{2}}\cdot\vec{e_{r}}$$ Ha pedig $r>R_{2}$: $$\vec{E}=0$$}} |
</wlatex></includeonly><noinclude> | </wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
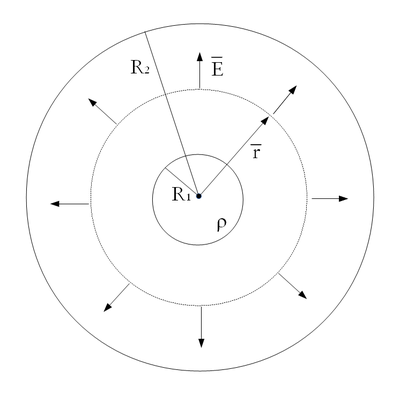
| + | [[Kép:KFGY2-1-10_a.png|none|400px]] | ||
| + | |||
'''a)''' | '''a)''' | ||
| − | |||
A gömb terét Gauss-törvénnyel határozzuk meg az előző feladatban alkalmazott módszerrel. | A gömb terét Gauss-törvénnyel határozzuk meg az előző feladatban alkalmazott módszerrel. | ||
| 29. sor: | 30. sor: | ||
$$\vec{E}\cdot 4\cdot r^{2}\cdot\pi = 0$$ | $$\vec{E}\cdot 4\cdot r^{2}\cdot\pi = 0$$ | ||
$$\vec{E}=0$$ | $$\vec{E}=0$$ | ||
| − | Mivel a | + | Mivel a megosztás következtében gömbhéj belső felületén jelenik meg ugyanakkora ellentétes előjelű töltés, mint amilyen amekkora az $R_{1}$ sugarú gömb töltése. |
| + | |||
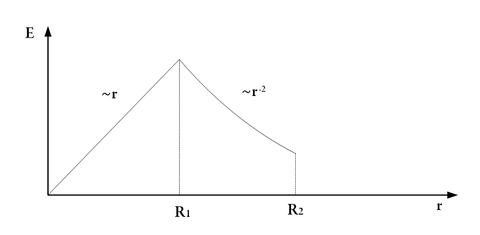
Ezt ábrázolva: | Ezt ábrázolva: | ||
| 36. sor: | 38. sor: | ||
'''b)''' | '''b)''' | ||
| − | Mivel a földelt | + | Mivel a földelt gömbhéj belső felületén lévő töltés abszolút értéke megegyezik az $R_{1}$ sugarú gömbön található töltés abszolútértékével, viszont előjele azzal ellentétes.Ezért |
| − | $$-4\cdot\pi\cdot R_{2}^{2}\cdot\ | + | $$-4\cdot\pi\cdot R_{2}^{2}\cdot\omega = \frac{4}{3}\cdot R_{1}^{3}\cdot\pi\cdot\rho$$ |
Amiből: | Amiből: | ||
| − | $$\ | + | $$\omega = -\frac{R_{1}^{3}\cdot\rho}{3\cdot R_{2}^{2}}$$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. szeptember 19., 18:10-kori változata
Feladat
- Egy
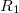sugarú gömben egyenletes 
térfogati töltéssűrűség van. Ezt egy 
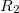sugarú földelt fémgömb veszi körül koncentrikus elrendezésben.
a) Határozzuk meg, a térerősséget a gömb középpontjától mért távolság függvényében, a gömbön belül és kívül!
b) Mekkora felületi töltéssűrűség alakul ki a földelt gömbhéj belső felületén?
Megoldás
a)
A gömb terét Gauss-törvénnyel határozzuk meg az előző feladatban alkalmazott módszerrel.
A Gauss-felület egy 
sugarú gömb, mely koncentrikus a töltéselrendezéssel. Ezek alapján a Gauss-tétel:
![\[\iint\vec{E}\cdot\vec{dA} = \frac{1}{\epsilon_{0}}\iiint\rho\cdot dV\]](/images/math/f/6/c/f6c18da3130637dc51790def87c0d576.png)
Ami ha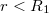 
:
![\[E\cdot 4\cdot r^{2}\cdot\pi = \frac{1}{\epsilon_{0}}\cdot\frac{4}{3}\cdot r^{3}\cdot\pi\cdot\rho\]](/images/math/5/2/c/52cdd4c3bf7ae3c6dd030316007c8758.png)
![\[\vec{E}=\frac{\rho\cdot r}{\epsilon_{0}\cdot 3}\cdot\vec{e_{r}}\]](/images/math/e/3/0/e30aec9803d933b7acabfb8843f72edb.png)
Ha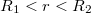 
::
![\[E\cdot 4\cdot r^{2}\cdot\pi = \frac{1}{\epsilon_{0}}\cdot\frac{4}{3}\cdot R^{3}\cdot\pi\cdot\rho\]](/images/math/6/8/0/680b0bb3fec39196fa4dc59e6d5d5f41.png)
![\[\vec{E}=\frac{\rho\cdot R^{3}}{\epsilon_{0}\cdot 3\cdot r^{2}}\cdot\vec{e_{r}}\]](/images/math/5/6/e/56e41121a5ed4c2cd4e68dbe29bfdc7a.png)
Ha pedig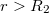 
:
![\[\vec{E}\cdot 4\cdot r^{2}\cdot\pi = 0\]](/images/math/b/e/e/bee187728fc69e215a36388a194ca8a6.png)
![\[\vec{E}=0\]](/images/math/2/c/d/2cd8159c5107d7b441bcba4a41bb2ea1.png)
Mivel a megosztás következtében gömbhéj belső felületén jelenik meg ugyanakkora ellentétes előjelű töltés, mint amilyen amekkora az 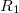sugarú gömb töltése.
Ezt ábrázolva:
b)
Mivel a földelt gömbhéj belső felületén lévő töltés abszolút értéke megegyezik az 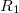sugarú gömbön található töltés abszolútértékével, viszont előjele azzal ellentétes.Ezért
![\[-4\cdot\pi\cdot R_{2}^{2}\cdot\omega = \frac{4}{3}\cdot R_{1}^{3}\cdot\pi\cdot\rho\]](/images/math/e/2/1/e21643652def17ddf47f8a735c48c05d.png)
Amiből:
![\[\omega = -\frac{R_{1}^{3}\cdot\rho}{3\cdot R_{2}^{2}}\]](/images/math/2/f/6/2f66054d8ade79df9cdca7f63f5839b8.png)
