Termodinamika példák - Dielektromos polarizáció termodinamikai vonatkozása
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Homogén rendszerek |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Mennyi hő szabadul fel az
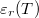 dielektromos állandójú dielektrikum polarizációjakor, ha a külső elektromos tér nagyságát állandó hőmérsékleten, kvázi-stacionáriusan növeljük nulláról egy nem túl nagy
dielektromos állandójú dielektrikum polarizációjakor, ha a külső elektromos tér nagyságát állandó hőmérsékleten, kvázi-stacionáriusan növeljük nulláról egy nem túl nagy  értékre? A térfogatváltozás elhanyagolható.
értékre? A térfogatváltozás elhanyagolható.
Megoldás
A felszabaduló hőt a termodinamika első főtételének segítségével tudjuk kifejezni, ahol be kell vezetnünk a munkavégzésre képes új konjugált változókat, az intenzív 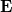 elektromos térerősséget és extenzív
elektromos térerősséget és extenzív 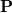 polarizációt. Ezt legegyszerűbben a változócsere során megállapított analógia alapján tehetjük meg:
polarizációt. Ezt legegyszerűbben a változócsere során megállapított analógia alapján tehetjük meg:
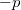 |
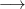 |
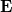 , ,
|
 |
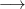 |
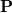 , ,
|
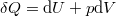 |
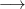 |
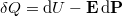 . .
|
Mivel a 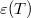 dielektromos állandó skalár, azért az elektromos térerősség és a polarizáció egymással párhuzamos,
dielektromos állandó skalár, azért az elektromos térerősség és a polarizáció egymással párhuzamos, 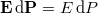 .
A hő kifejezéséhez meg kell adnunk a belső energia megváltozását teljes differenciálként a két ismert paraméter, a hőmérséklet és a polarizáció segítségével (a feladat szerint a térfogatváltozást elhanyagolhatjuk):
.
A hő kifejezéséhez meg kell adnunk a belső energia megváltozását teljes differenciálként a két ismert paraméter, a hőmérséklet és a polarizáció segítségével (a feladat szerint a térfogatváltozást elhanyagolhatjuk):
![\[ \mathrm{d}U = \left(\frac{\partial U}{\partial T}\right)_P\,\mathrm{d}T + \left(\frac{\partial U}{\partial P}\right)_T\,\mathrm{d}P, \]](/images/math/c/0/2/c027105afdf2ee611cd78479d4e0fc82.png)
ahol a második paramétert a változócseréről szóló feladatban levezetett általános képlet alapján felírhatjuk:
![\[ \left(\frac{\partial U}{\partial P}\right)_T = -T\left(\frac{\partial E}{\partial T}\right)_P + E. \]](/images/math/0/d/2/0d2001072e363ec7a2f8e66172c18940.png)
Mivel az elektromos teret állandó hőmérséklet mellet kapcsoljuk be, 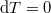 , a hő kifejezésében egyetlen tag marad:
, a hő kifejezésében egyetlen tag marad:
![\[ \delta Q = -T\left(\frac{\partial E}{\partial T}\right)_P \,\mathrm{d}P. \]](/images/math/2/8/e/28efcafdbe3df41b8167bd9297b45ec7.png)
A differenciálhányados kiszámításához az elektromos teret meg kell adnunk a hőmérséklet és a polarizáció függvényeként. Ehhez az összefüggéshez a polarizáció (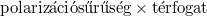 ) definíciójából indulunk ki:
) definíciójából indulunk ki:
![\[ P = \varepsilon_0\left(\varepsilon_r(T)-1\right)E\,V, \]](/images/math/a/0/a/a0a444b5016c32a14ec79b2aaff9639e.png)
amiből
![\[ E(T,P) = \frac{P}{\varepsilon_0\left(\varepsilon_r(T)-1\right)V} \qquad \text{és} \qquad \left(\frac{\partial E}{\partial T}\right)_P = - \frac{P}{\varepsilon_0V} \frac{1}{\left(\varepsilon_r(T)-1\right)^2} \frac{\partial \varepsilon}{\partial T}. \]](/images/math/6/d/a/6da303cfd48dc2038fa4b307137c56ee.png)
Ezzel
![\[ \delta Q = \frac{T}{\varepsilon_0V\left(\varepsilon_r(T)-1\right)^2} \frac{\partial \varepsilon_r(T)}{\partial T} \cdot P \,\mathrm{d}P, \]](/images/math/3/b/2/3b28b9d5b95018e8129285a5f7c61151.png)
amit állandó hőmérsékleten integrálhatunk, mert akkor az első tényező is állandó (magas hőmérsékleten 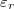 valóban nem függ
valóban nem függ  -től, azaz
-től, azaz  -től):
-től):
![\[ Q = \frac{T}{\varepsilon_0V\left(\varepsilon_r(T)-1\right)^2} \frac{\partial \varepsilon_r(T)}{\partial T} \frac{P^2}{2}. \]](/images/math/1/c/8/1c8049d1bf757680b0e3bed1d8e6f9ec.png)
Ide a polarizáció definícióját visszahelyettesítve
![\[ Q=-\frac12T\frac{\mathrm{d}\varepsilon_r(T)}{\mathrm{d}T}\varepsilon_0E^2V \]](/images/math/9/1/7/917eaa05505cf5470cb04667a8e6ce38.png)
egyszerűbb alakot nyerjük.
Megjegyzés
Eredményünk az elektromos eltolás 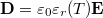 definíciójával
definíciójával
![\[ Q=-\frac12\mathbf{DE}\frac{T}{\varepsilon_r(T)}\frac{\mathrm{d}\varepsilon_r(T)}{\mathrm{d}T}V \]](/images/math/6/f/e/6fe4da0d1c2e1910a8f629af64a196b7.png)
vektoros alakban is érvényes.