Termodinamika példák - Entrópia és entalpia állapotegyenlettel
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Homogén rendszerek |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy rendszer állapotegyenlete
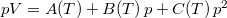 , ahol a hőmérsékletfüggő együtthatók kísérletekből ismertek. Mennyit változik a rendszer szabad entalpiája és entrópiája, ha a nyomást rögzített
, ahol a hőmérsékletfüggő együtthatók kísérletekből ismertek. Mennyit változik a rendszer szabad entalpiája és entrópiája, ha a nyomást rögzített  hőmérsékleten
hőmérsékleten 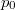 -ról
-ról 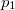 -re változtatjuk?
-re változtatjuk?
Megoldás
A termodinamika differenciális összefüggései segítségével megteremthetjük a kapcolatot a szabadentalpia és a felírt állapotegyenlet között:
![\[ \left(\frac{\partial G}{\partial p}\right)_T=V,\]](/images/math/8/c/a/8ca161d80df2e851e656929408509758.png)
mert az állapotegyenletből  kifejezhető
kifejezhető  és
és  segítségével:
segítségével:
![\[ V=\frac{A\left(T\right)} p+B\left(T\right)+C\left(T\right)p. \]](/images/math/f/2/d/f2d6c676596ed26c9e447b30489fa42e.png)
Ezt integrálva 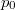 és
és 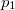 határok között:
határok között:
![\[ \Delta G=A\left(T\right)\ln \frac{p_1}{p_0}+B\left(T\right)\left(p_1-p_0\right)+\frac12 C\left(T\right)\left( p_1^2- p_0^2\right). \]](/images/math/f/9/4/f944ea519d2ec733b79a7b5b05b3b1a9.png)
Az entrópiára vonatkozó megfelelő differenciális összefüggés:
![\[ \left(\frac{\partial G}{\partial T}\right)_p = -S, \]](/images/math/6/6/a/66acce1c36871ccce192959036627384.png)
amivel
![\[ \Delta S=\frac{\mathrm{d}A(T)}{\mathrm{d}T}\ln \frac{p_0}{p_1}+\frac{\mathrm{d}B(T)}{\mathrm{d}T}\left(p_0-p_1\right)+\frac12 \frac{\mathrm{d}C(T)}{\mathrm{d}T}\left(p_0^2-p_1^2\right). \]](/images/math/9/1/2/91208fd371bc1fd71d83bc75d243454d.png)