Termodinamika példák - Hőmérsékletváltozás mérhető mennyiségekkel adiabatikus tágulásban
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Homogén rendszerek |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Fejezzük ki mérhető mennyiségekkel (hőtágulási együttható, kompresszibilitás, mólhő) egy rendszer
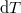 hőmérséklet-változását, ha térfogata adiabatikus, kvázisztatikus folyamat során
hőmérséklet-változását, ha térfogata adiabatikus, kvázisztatikus folyamat során 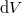 -vel megváltozik! Mutassuk meg, hogy
-vel megváltozik! Mutassuk meg, hogy 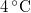 alatt a víz adiabatikus, kvázisztatikus összenyomáskor lehűl!
alatt a víz adiabatikus, kvázisztatikus összenyomáskor lehűl!
Megoldás
Az első főtétel
![\[ \mathrm{d}U = T\,\mathrm{d}S - p\,\mathrm{d}V \]](/images/math/d/d/8/dd8451043d8139e9eac92b78b7bb4805.png)
adiabatikus folyamatra egyszerűsödik:
![\[ \mathrm{d}U = - p\,\mathrm{d}V. \]](/images/math/f/4/0/f400341b0db6f9931c0c1e47f7318aad.png)
Ezt egyenlővé téve 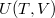
![\[ \mathrm{d}U = \left(\frac{\partial U}{\partial T}\right)_V\,\mathrm{d}T + \left(\frac{\partial U}{\partial V}\right)_T\,\mathrm{d}V\]](/images/math/a/f/e/afe6daafddfefdf1c50ffb68ff0c212c.png)
alakú teljes differenciáljával és felhasználva 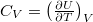 definíciót
definíciót
![\[ -p\,\mathrm{d}V = C_V\,\mathrm{d}T + \left(\frac{\partial U}{\partial V}\right)_T\,\mathrm{d}V \]](/images/math/c/f/0/cf08a82fc1497090a39526d7a5348af3.png)
egyenletet kapjuk.
Az általános változócseréről szóló feladatból ismerjük (vagy egy következő feladat alapján kifejezhetjük) a belső energia térfogatfüggésére vonatkozó differenciális összefüggést:
![\[ \left(\frac{\partial U}{\partial V}\right)_T = T \left(\frac{\partial p}{\partial T}\right)_V-p,\]](/images/math/3/f/a/3fa36d0c2000c91782c525c3d04f8dc2.png)
így az egyenletünk
![\[ 0 = C_V\,\mathrm{d}T+T{\left(\frac{\partial p}{\partial T}\right)}_V\,\mathrm{d}V. \]](/images/math/a/3/4/a343a5da4df4ff63f47276447613ea5d.png)
A nyomás hőmérsékletfüggéséről szóló feladat
![\[ \left(\frac{\partial p}{\partial T}\right)_V = \frac{\beta_p}{\kappa_T} \]](/images/math/6/d/0/6d06e64082b87d57e19f008be86e2f00.png)
eredményét felhasználva:
![\[ 0 = C_V\,\mathrm{d}T + T\frac{\beta_p}{\kappa_T}\,\mathrm{d}V, \]](/images/math/d/a/d/dadf8f8b5faa551ebfb216a447565e91.png)
amiből
![\[ \mathrm{d}T = -T\frac{\beta_p}{\kappa_T C_V}\,\mathrm{d}V. \]](/images/math/1/4/f/14f9ac865ebd892aa4587ea4166a3ffe.png)
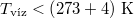 hőmérsékleten a víz hőtágulási együtthatója negatív (
hőmérsékleten a víz hőtágulási együtthatója negatív (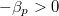 ), ezért adiabatikus összenyomásra (
), ezért adiabatikus összenyomásra (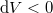 ) a hőmérsékletváltozás
) a hőmérsékletváltozás
![\[ \mathrm{d}T < 0, \]](/images/math/1/d/e/1debf7c9091065bf1ed11dc054b93afa.png)
hiszen a többi tényező pozitív.