„Termodinamika példák - A termodinamika differenciális összefüggései” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger [[Kategória:Termodinamika - Kinetikus gázelmélet, transzportfolyamatok]…”)
 
(→‎Megoldás)
 
(2 szerkesztő 10 közbeeső változata nincs mutatva)
9. sor: 9. sor:
 
}}
 
}}
 
== Feladat ==
 
== Feladat ==
−
</noinclude><wlatex># Bizonyítsuk be a $\left(\frac{\partial F}{\partial V}\right)_T=-p$, $\left(\frac{\partial F}{\partial T}\right)_V=-S$, $\left(\frac{\partial G}{\partial p}\right)_T=V$ és $\left(\frac{\partial G}{\partial T}\right)_p=-S$ összefüggéseket!
+
</noinclude><wlatex># Bizonyítsuk be a $\displaystyle \left(\frac{\partial F}{\partial V}\right)_T=-p$, $\displaystyle \left(\frac{\partial F}{\partial T}\right)_V=-S$, $\displaystyle \left(\frac{\partial G}{\partial p}\right)_T=V$ és $\displaystyle \left(\frac{\partial G}{\partial T}\right)_p=-S$ összefüggéseket!
 
</wlatex><noinclude>
 
</wlatex><noinclude>
 +
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>Megoldás szövege
+
<wlatex>Számításainkat nem csak a feladatban előírt, hanem minden termodinamikai potenciálra elvégezzük. Amikor a termodinamikai potenciálok az alább megjelölt természetes változóikkal függvényeként vannak kifejezve, a termodinamika fundamentális függvényeinek is szokás őket nevezni.
 +
 
 +
=== Belső energia ===
 +
(''Megjegyezzük, hogy a $\lambda U(S,V,N)=U(\lambda S,\lambda V,\lambda N)$ Euler-egyenlet megoldásaként $U(S,V,N)= TS-pV+\mu N$ expliciten felírható, de erre a függvényalakra az alábbi tárgyalásban nincs szükség.'')
 +
$$ \boxed{U(S,V,N)} $$
 +
$$ \mathrm{d}U = T\,\mathrm{d}S-p\,\mathrm{d}V+\mu\,\mathrm{d}N$$
 +
$$ \left(\frac{\partial U}{\partial S}\right)_{V,N} = T, \qquad \left(\frac{\partial U}{\partial V}\right)_{S,N} = -p, $$
 +
$$ \left(\frac{\partial U}{\partial N}\right)_{V,S} = \mu. $$
 +
''A továbbiakban a kémiai potenciáltól és részecskeszámtól való függést nem írjuk ki.''
 +
 
 +
A termodinamikai potenciálokon hajtsuk végre a [http://en.wikipedia.org/wiki/Legendre_transformation Legendre-transzformációt], ezt az alakot vessük össze a potenciál teljes differenciáljával:
 +
 
 +
=== ''Helmholtz''-féle szabadenergia ===
 +
(''Régiesen exergiának is nevezik. Elterjedt ekvivalens jelölése $F(T,V)\equiv A(T,V)$, ami főleg külföldi szakirodalomban jelenik meg.'')
 +
$$ \boxed{F(T,V)=U-TS} $$
 +
$$ \mathrm{d}F = \mathrm{d}U-S\,\mathrm{d}T-T\,\mathrm{d}S
 +
    = -S\,\mathrm{d}T - p\,\mathrm{d}V
 +
    = \left(\frac{\partial F}{\partial T}\right)_V \mathrm{d}T + \left(\frac{\partial F}{\partial V}\right)_T \mathrm{d}V, $$
 +
$$ \left(\frac{\partial F}{\partial T}\right)_V = -S, \qquad \left(\frac{\partial F}{\partial V}\right)_T = -p. $$
 +
 
 +
 
 +
=== Entalpia ===
 +
(''Ezt a függvényt ''Gibbs'' alkotta meg, de az elnevezése későbbről származik.'')
 +
$$ \boxed{H(S,p)=U+pV} $$
 +
$$ \mathrm{d}H = \mathrm{d}U+V\,\mathrm{d}p+p\,\mathrm{d}V
 +
    = T\,\mathrm{d}S + V\,\mathrm{d}p
 +
    = \left(\frac{\partial H}{\partial S}\right)_p \mathrm{d}S + \left(\frac{\partial H}{\partial p}\right)_S \mathrm{d}p, $$
 +
$$ \left(\frac{\partial H}{\partial S}\right)_p = T, \qquad \left(\frac{\partial H}{\partial p}\right)_S = V. $$
 +
 
 +
 
 +
=== Szabadentalpia ===
 +
(''Szokás még ''Gibbs''-féle szabadenergiának is nevezni.'')
 +
$$ \boxed{G(T,p)=H-TS=U+pV-TS} $$
 +
$$ \mathrm{d}G = \mathrm{d}U+V\,\mathrm{d}p+p\,\mathrm{d}V-S\,\mathrm{d}T-T\,\mathrm{d}S
 +
    = -S\,\mathrm{d}T + V\,\mathrm{d}p
 +
    = \left(\frac{\partial G}{\partial T}\right)_p \mathrm{d}T + \left(\frac{\partial G}{\partial p}\right)_T \mathrm{d}p, $$
 +
$$ \left(\frac{\partial G}{\partial T}\right)_p=-S, \qquad \left(\frac{\partial G}{\partial p}\right)_T=V. $$
 +
 
 +
''Megjegyezzük, hogy a szabadentalpia szoros kapcsolatban áll a kémiai potenciállal: $G(T,p,N)=\mu(T,p)\cdot N$ és $\left(\frac{\partial G}{\partial N}\right)_{T,p}=\mu$.''
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap jelenlegi, 2024. november 11., 16:47-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Homogén rendszerek
Feladatok listája:
  1. TD diffegyenletek
  2. Maxwell-relációk
  3. Általános változócsere
  4. dT(S=áll) mérhetőkkel
  5. TdS mérhetőkkel
  6. Állapotjelzők (V,S) fv-ei
  7. dS(p=áll) mérhetőkkel
  8. Potenciálok állapotegyenletből
  9. Gumiszalag TD potenciáljai
  10. Dielektromos polarizáció
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

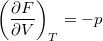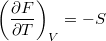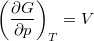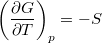  1. Bizonyítsuk be a \setbox0\hbox{$\displaystyle \left(\frac{\partial F}{\partial V}\right)_T=-p$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$\displaystyle \left(\frac{\partial F}{\partial T}\right)_V=-S$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$\displaystyle \left(\frac{\partial G}{\partial p}\right)_T=V$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\displaystyle \left(\frac{\partial G}{\partial T}\right)_p=-S$}% \message{//depth:\the\dp0//}% \box0% összefüggéseket!

Megoldás

Számításainkat nem csak a feladatban előírt, hanem minden termodinamikai potenciálra elvégezzük. Amikor a termodinamikai potenciálok az alább megjelölt természetes változóikkal függvényeként vannak kifejezve, a termodinamika fundamentális függvényeinek is szokás őket nevezni.

Belső energia

(Megjegyezzük, hogy a 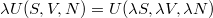\setbox0\hbox{$\lambda U(S,V,N)=U(\lambda S,\lambda V,\lambda N)$}% \message{//depth:\the\dp0//}% \box0% Euler-egyenlet megoldásaként 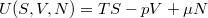\setbox0\hbox{$U(S,V,N)= TS-pV+\mu N$}% \message{//depth:\the\dp0//}% \box0% expliciten felírható, de erre a függvényalakra az alábbi tárgyalásban nincs szükség.)

\[ \boxed{U(S,V,N)} \]
\[ \mathrm{d}U = T\,\mathrm{d}S-p\,\mathrm{d}V+\mu\,\mathrm{d}N\]
\[ \left(\frac{\partial U}{\partial S}\right)_{V,N} = T, \qquad \left(\frac{\partial U}{\partial V}\right)_{S,N} = -p, \]
\[ \left(\frac{\partial U}{\partial N}\right)_{V,S} = \mu. \]

A továbbiakban a kémiai potenciáltól és részecskeszámtól való függést nem írjuk ki.

A termodinamikai potenciálokon hajtsuk végre a Legendre-transzformációt, ezt az alakot vessük össze a potenciál teljes differenciáljával:

Helmholtz-féle szabadenergia

(Régiesen exergiának is nevezik. Elterjedt ekvivalens jelölése 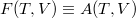\setbox0\hbox{$F(T,V)\equiv A(T,V)$}% \message{//depth:\the\dp0//}% \box0%, ami főleg külföldi szakirodalomban jelenik meg.)

\[ \boxed{F(T,V)=U-TS} \]
\[ \mathrm{d}F = \mathrm{d}U-S\,\mathrm{d}T-T\,\mathrm{d}S = -S\,\mathrm{d}T - p\,\mathrm{d}V = \left(\frac{\partial F}{\partial T}\right)_V \mathrm{d}T + \left(\frac{\partial F}{\partial V}\right)_T \mathrm{d}V, \]
\[ \left(\frac{\partial F}{\partial T}\right)_V = -S, \qquad \left(\frac{\partial F}{\partial V}\right)_T = -p. \]


Entalpia

(Ezt a függvényt Gibbs alkotta meg, de az elnevezése későbbről származik.)

\[ \boxed{H(S,p)=U+pV} \]
\[ \mathrm{d}H = \mathrm{d}U+V\,\mathrm{d}p+p\,\mathrm{d}V = T\,\mathrm{d}S + V\,\mathrm{d}p = \left(\frac{\partial H}{\partial S}\right)_p \mathrm{d}S + \left(\frac{\partial H}{\partial p}\right)_S \mathrm{d}p, \]
\[ \left(\frac{\partial H}{\partial S}\right)_p = T, \qquad \left(\frac{\partial H}{\partial p}\right)_S = V. \]


Szabadentalpia

(Szokás még Gibbs-féle szabadenergiának is nevezni.)

\[ \boxed{G(T,p)=H-TS=U+pV-TS} \]
\[ \mathrm{d}G = \mathrm{d}U+V\,\mathrm{d}p+p\,\mathrm{d}V-S\,\mathrm{d}T-T\,\mathrm{d}S = -S\,\mathrm{d}T + V\,\mathrm{d}p = \left(\frac{\partial G}{\partial T}\right)_p \mathrm{d}T + \left(\frac{\partial G}{\partial p}\right)_T \mathrm{d}p, \]
\[ \left(\frac{\partial G}{\partial T}\right)_p=-S, \qquad \left(\frac{\partial G}{\partial p}\right)_T=V. \]

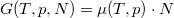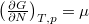Megjegyezzük, hogy a szabadentalpia szoros kapcsolatban áll a kémiai potenciállal: \setbox0\hbox{$G(T,p,N)=\mu(T,p)\cdot N$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\left(\frac{\partial G}{\partial N}\right)_{T,p}=\mu$}% \message{//depth:\the\dp0//}% \box0%.

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Termodinamika_példák_-_A_termodinamika_differenciális_összefüggései&oldid=29445”