„Termodinamika példák - A termodinamika differenciális összefüggései” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger [[Kategória:Termodinamika - Kinetikus gázelmélet, transzportfolyamatok]…”)
 
9. sor: 9. sor:
 
}}
 
}}
 
== Feladat ==
 
== Feladat ==
−
</noinclude><wlatex># Bizonyítsuk be a $\left(\frac{\partial F}{\partial V}\right)_T=-p$, $\left(\frac{\partial F}{\partial T}\right)_V=-S$, $\left(\frac{\partial G}{\partial p}\right)_T=V$ és $\left(\frac{\partial G}{\partial T}\right)_p=-S$ összefüggéseket!
+
</noinclude><wlatex># Bizonyítsuk be a $\displaystyle \left(\frac{\partial F}{\partial V}\right)_T=-p$, $\displaystyle \left(\frac{\partial F}{\partial T}\right)_V=-S$, $\displaystyle \left(\frac{\partial G}{\partial p}\right)_T=V$ és $\displaystyle \left(\frac{\partial G}{\partial T}\right)_p=-S$ összefüggéseket!
 
</wlatex><noinclude>
 
</wlatex><noinclude>
 
== Megoldás ==
 
== Megoldás ==

A lap 2013. április 16., 12:47-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Homogén rendszerek
Feladatok listája:
  1. TD diffegyenletek
  2. Maxwell-relációk
  3. Általános változócsere
  4. dT(S=áll) mérhetőkkel
  5. TdS mérhetőkkel
  6. Állapotjelzők (V,S) fv-ei
  7. dS(p=áll) mérhetőkkel
  8. Potenciálok állapotegyenletből
  9. Gumiszalag TD potenciáljai
  10. Dielektromos polarizáció
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

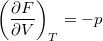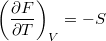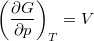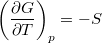  1. Bizonyítsuk be a \setbox0\hbox{$\displaystyle \left(\frac{\partial F}{\partial V}\right)_T=-p$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$\displaystyle \left(\frac{\partial F}{\partial T}\right)_V=-S$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$\displaystyle \left(\frac{\partial G}{\partial p}\right)_T=V$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\displaystyle \left(\frac{\partial G}{\partial T}\right)_p=-S$}% \message{//depth:\the\dp0//}% \box0% összefüggéseket!

Megoldás

Megoldás szövege

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Termodinamika_példák_-_A_termodinamika_differenciális_összefüggései&oldid=8896”