„Termodinamika példák - A termodinamika differenciális összefüggései” változatai közötti eltérés

A Fizipedia wikiből
12. sor: 12. sor:
 
</wlatex><noinclude>
 
</wlatex><noinclude>
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>Megoldás szövege
+
<wlatex>$$\framebox {$U(S,V,N) = TS-pV+\mu N$}$$
 +
$$ \mathrm{d}U = T\,\mathrm{d}S-p\,\mathrm{d}V+\mu\,\mathrm{d}N$$
 +
$$ \left(\frac{\partial U}{\partial S}\right)_V = T, \qquad \left(\frac{\partial U}{\partial V}\right)_S = -p. $$
 +
''A továbbiakban a kémiai potenciáltól és részecskeszámtól való függést nem írjuk ki.''
 +
 
 +
A termodinamikai potenciálokon hajtsuk végre a [http://en.wikipedia.org/wiki/Legendre_transformation Legendre-transzformációt], ezt az alakot vessük össze a potenciál teljes differenciáljával:
 +
 
 +
$$ \framebox{$F(T,V)=U-TS$} $$
 +
$$ \mathrm{d}F = \mathrm{d}U-S\,\mathrm{d}T-T\,\mathrm{d}S
 +
    = -S\,\mathrm{d}T - p\,\mathrm{d}V
 +
    = \left(\frac{\partial F}{\partial T}\right)_V \mathrm{d}T + \left(\frac{\partial F}{\partial V}\right)_T \mathrm{d}V, $$
 +
$$ \left(\frac{\partial F}{\partial T}\right)_V = -S, \qquad \left(\frac{\partial F}{\partial V}\right)_T = -p. $$
 +
 
 +
 
 +
$$ \framebox{$H(S,p)=U+pV$} $$
 +
$$ \mathrm{d}H = \mathrm{d}U+V\,\mathrm{d}p+p\,\mathrm{d}V
 +
    = T\,\mathrm{d}S + V\,\mathrm{d}p
 +
    = \left(\frac{\partial H}{\partial S}\right)_p \mathrm{d}S + \left(\frac{\partial H}{\partial p}\right)_S \mathrm{d}p, $$
 +
$$ \left(\frac{\partial H}{\partial S}\right)_p = T, \qquad \left(\frac{\partial H}{\partial p}\right)_S = V. $$
 +
 
 +
 
 +
$$ \framebox{$G(T,p)=H-TS=U+pV-TS$} $$
 +
$$ \mathrm{d}G = \mathrm{d}U+V\,\mathrm{d}p+p\,\mathrm{d}V-S\,\mathrm{d}T-T\,\mathrm{d}S
 +
    = -S\,\mathrm{d}T + V\,\mathrm{d}p
 +
    = \left(\frac{\partial G}{\partial T}\right)_p \mathrm{d}T + \left(\frac{\partial G}{\partial p}\right)_T \mathrm{d}p, $$
 +
$$ \left(\frac{\partial G}{\partial T}\right)_p=-S, \qquad \left(\frac{\partial G}{\partial p}\right)_T=V. $$
 +
 
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap 2013. április 16., 13:55-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Homogén rendszerek
Feladatok listája:
  1. TD diffegyenletek
  2. Maxwell-relációk
  3. Általános változócsere
  4. dT(S=áll) mérhetőkkel
  5. TdS mérhetőkkel
  6. Állapotjelzők (V,S) fv-ei
  7. dS(p=áll) mérhetőkkel
  8. Potenciálok állapotegyenletből
  9. Gumiszalag TD potenciáljai
  10. Dielektromos polarizáció
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

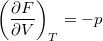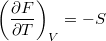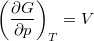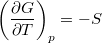  1. Bizonyítsuk be a \setbox0\hbox{$\displaystyle \left(\frac{\partial F}{\partial V}\right)_T=-p$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$\displaystyle \left(\frac{\partial F}{\partial T}\right)_V=-S$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$\displaystyle \left(\frac{\partial G}{\partial p}\right)_T=V$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\displaystyle \left(\frac{\partial G}{\partial T}\right)_p=-S$}% \message{//depth:\the\dp0//}% \box0% összefüggéseket!

Megoldás

\[\framebox {$U(S,V,N) = TS-pV+\mu N$}\]
\[ \mathrm{d}U = T\,\mathrm{d}S-p\,\mathrm{d}V+\mu\,\mathrm{d}N\]
\[ \left(\frac{\partial U}{\partial S}\right)_V = T, \qquad \left(\frac{\partial U}{\partial V}\right)_S = -p. \]

A továbbiakban a kémiai potenciáltól és részecskeszámtól való függést nem írjuk ki.

A termodinamikai potenciálokon hajtsuk végre a Legendre-transzformációt, ezt az alakot vessük össze a potenciál teljes differenciáljával:

\[ \framebox{$F(T,V)=U-TS$} \]
\[ \mathrm{d}F = \mathrm{d}U-S\,\mathrm{d}T-T\,\mathrm{d}S = -S\,\mathrm{d}T - p\,\mathrm{d}V = \left(\frac{\partial F}{\partial T}\right)_V \mathrm{d}T + \left(\frac{\partial F}{\partial V}\right)_T \mathrm{d}V, \]
\[ \left(\frac{\partial F}{\partial T}\right)_V = -S, \qquad \left(\frac{\partial F}{\partial V}\right)_T = -p. \]


\[ \framebox{$H(S,p)=U+pV$} \]
\[ \mathrm{d}H = \mathrm{d}U+V\,\mathrm{d}p+p\,\mathrm{d}V = T\,\mathrm{d}S + V\,\mathrm{d}p = \left(\frac{\partial H}{\partial S}\right)_p \mathrm{d}S + \left(\frac{\partial H}{\partial p}\right)_S \mathrm{d}p, \]
\[ \left(\frac{\partial H}{\partial S}\right)_p = T, \qquad \left(\frac{\partial H}{\partial p}\right)_S = V. \]


\[ \framebox{$G(T,p)=H-TS=U+pV-TS$} \]
\[ \mathrm{d}G = \mathrm{d}U+V\,\mathrm{d}p+p\,\mathrm{d}V-S\,\mathrm{d}T-T\,\mathrm{d}S = -S\,\mathrm{d}T + V\,\mathrm{d}p = \left(\frac{\partial G}{\partial T}\right)_p \mathrm{d}T + \left(\frac{\partial G}{\partial p}\right)_T \mathrm{d}p, \]
\[ \left(\frac{\partial G}{\partial T}\right)_p=-S, \qquad \left(\frac{\partial G}{\partial p}\right)_T=V. \]


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Termodinamika_példák_-_A_termodinamika_differenciális_összefüggései&oldid=8913”