„Mechanika - Rugók kapcsolása” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
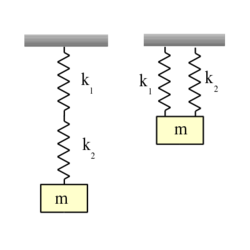
| − | </noinclude><wlatex># (6.7.) Határozzuk meg a nehézségi erőtérben az ábrán látható módon a $k_1$ és $k_2$ direkciós erejű rugókra erősített $m$ tömegű test rezgési frekvenciáit! | + | </noinclude><wlatex># (6.7.) Határozzuk meg a nehézségi erőtérben az ábrán látható módon a $k_1$ és $k_2$ direkciós erejű rugókra erősített $m$ tömegű test rezgési frekvenciáit! [[Kép:Kfgy1_6_7.svg|none|250px]]</wlatex><includeonly><wlatex>{{Útmutatás|content=Írjuk fel a test mozgásegyenletét mindkét esetben, és határozzunk meg effektív rugólállandókat!}}{{Végeredmény|content=$$\omega=2\pi f=\sqrt{\frac{k_{\rm{eff}}}m},$$ ahol $$k_{\rm{eff}}=k_1+k_2,$$ illetve $$\frac1{k_{\rm{eff}}}=\frac1{k_1}+\frac1{k_2}$$}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>Az állandó nehézségi erőtér csak a rezgés egyensúlyi helyzetét tolja el, a rezgés frekvenciáját nem befolyásolja, ezért ezt a mozgásegyenletekből elhagyhatjuk. A feladat lényege a sorosan vagy párhuzamosan kapcsolt rugók $k_{\rm{eff}}$ eredő rugóállandójának meghatározása. Párhuzamos esetben a mozgásegyenlet $$m\ddot x=-k_1m-k_2m=-(k_1+k_2)m,$$ ebből az eredő rugóállandó $$k_{\rm{eff}}=k_1+k_2,$$ azaz több párhuzamosan kapcsolt rugó esetén a rugóállandók összeadódnak. A rezgés körfrekvenciája $$\omega=\sqrt{\frac{k_{\rm{eff}}}m}$$ Soros esetben a két rugót feszítő $F$ erő azonos, hisz a kettejük érintezésénél lévő erőpárnak azonos nagyságúnak kell lennie (Newton III. axióma!). Ez az $F$ erő hat az $m$ tömegre is, így a mozgásegyenlet $$m\ddot x=F=k_1x_1=k_2x_2=k_{\rm{eff}}x,$$ ahol $x_1$ és $x_2$ a két rugó megnyúlása, $x=x_1+x_2$ pedig a test elmozdulása, egyben a rugólánc teljes megnyúlása. Az egyenlet utolsó kifejezése maga az eredő rugóállandó definíciója is egyben. Továbbírva az egyenletet $$F=k_{\rm{eff}}(x_1+x_2)=k_{\rm{eff}}(\frac F{k_1}+\frac F{k_2}),$$ melyet $F$-el egyszerűsítve és rendezve kapjuk $$\frac1{k_{\rm{eff}}}=\frac1{k_1}+\frac1{k_2},$$ általános esetben pedig reciprok összegzési szabályt kaphatunk a sorba kapcsolt rugókra.</wlatex> | <wlatex>Az állandó nehézségi erőtér csak a rezgés egyensúlyi helyzetét tolja el, a rezgés frekvenciáját nem befolyásolja, ezért ezt a mozgásegyenletekből elhagyhatjuk. A feladat lényege a sorosan vagy párhuzamosan kapcsolt rugók $k_{\rm{eff}}$ eredő rugóállandójának meghatározása. Párhuzamos esetben a mozgásegyenlet $$m\ddot x=-k_1m-k_2m=-(k_1+k_2)m,$$ ebből az eredő rugóállandó $$k_{\rm{eff}}=k_1+k_2,$$ azaz több párhuzamosan kapcsolt rugó esetén a rugóállandók összeadódnak. A rezgés körfrekvenciája $$\omega=\sqrt{\frac{k_{\rm{eff}}}m}$$ Soros esetben a két rugót feszítő $F$ erő azonos, hisz a kettejük érintezésénél lévő erőpárnak azonos nagyságúnak kell lennie (Newton III. axióma!). Ez az $F$ erő hat az $m$ tömegre is, így a mozgásegyenlet $$m\ddot x=F=k_1x_1=k_2x_2=k_{\rm{eff}}x,$$ ahol $x_1$ és $x_2$ a két rugó megnyúlása, $x=x_1+x_2$ pedig a test elmozdulása, egyben a rugólánc teljes megnyúlása. Az egyenlet utolsó kifejezése maga az eredő rugóállandó definíciója is egyben. Továbbírva az egyenletet $$F=k_{\rm{eff}}(x_1+x_2)=k_{\rm{eff}}(\frac F{k_1}+\frac F{k_2}),$$ melyet $F$-el egyszerűsítve és rendezve kapjuk $$\frac1{k_{\rm{eff}}}=\frac1{k_1}+\frac1{k_2},$$ általános esetben pedig reciprok összegzési szabályt kaphatunk a sorba kapcsolt rugókra.</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. június 24., 21:09-kori változata
Feladat
- (6.7.) Határozzuk meg a nehézségi erőtérben az ábrán látható módon a
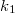és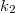 
direkciós erejű rugókra erősített 
tömegű test rezgési frekvenciáit! 
Megoldás
Az állandó nehézségi erőtér csak a rezgés egyensúlyi helyzetét tolja el, a rezgés frekvenciáját nem befolyásolja, ezért ezt a mozgásegyenletekből elhagyhatjuk. A feladat lényege a sorosan vagy párhuzamosan kapcsolt rugók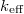
eredő rugóállandójának meghatározása. Párhuzamos esetben a mozgásegyenlet ![\[m\ddot x=-k_1m-k_2m=-(k_1+k_2)m,\]](/images/math/2/b/4/2b442fa3e47c48b4a175cdadb64861fb.png)
![\[k_{\rm{eff}}=k_1+k_2,\]](/images/math/4/5/7/4573653343b4a62118c0aa51078a26d9.png)
![\[\omega=\sqrt{\frac{k_{\rm{eff}}}m}\]](/images/math/6/4/3/643a8762b342f5fdd44fe6e4c4e77944.png)
erő azonos, hisz a kettejük érintezésénél lévő erőpárnak azonos nagyságúnak kell lennie (Newton III. axióma!). Ez az erő hat az tömegre is, így a mozgásegyenlet ![\[m\ddot x=F=k_1x_1=k_2x_2=k_{\rm{eff}}x,\]](/images/math/8/0/a/80ae1e3b01b08f329d0a6962d6516b2b.png)
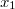és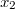 
a két rugó megnyúlása, 
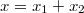pedig a test elmozdulása, egyben a rugólánc teljes megnyúlása. Az egyenlet utolsó kifejezése maga az eredő rugóállandó definíciója is egyben. Továbbírva az egyenletet ![\[F=k_{\rm{eff}}(x_1+x_2)=k_{\rm{eff}}(\frac F{k_1}+\frac F{k_2}),\]](/images/math/c/d/9/cd976752ee480dd212b668f80afcdf6e.png)
-el egyszerűsítve és rendezve kapjuk ![\[\frac1{k_{\rm{eff}}}=\frac1{k_1}+\frac1{k_2},\]](/images/math/c/9/1/c911f42f5df197723476064d4836a638.png)
