„Mechanika - Test rugók között” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
(→Megoldás) |
||
| 11. sor: | 11. sor: | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>Ha a testet kissé kimozdítjuk egyensúlyi helyzetéből, az egyik rugó húzni, a másik nyomni fogja, azaz a két rugóerő azonos írányú, így a test mozgásegyenlete $$m\ddot x=-k_1x-k_2x,$$ ami megfelel a párhuzamosan kapcsolt rugók esetének, ahol a két rugóállandó összege adja az eredő rugóállandót.</wlatex> | + | <wlatex>Ha a testet kissé kimozdítjuk egyensúlyi helyzetéből, az egyik rugó húzni, a másik nyomni fogja, azaz a két rugóerő azonos írányú, így a test mozgásegyenlete $$m\ddot x=-k_1x-k_2x,$$ ami megfelel a párhuzamosan kapcsolt rugók esetének, ahol a két rugóállandó összege adja az eredő rugóállandót, így $\omega=\sqrt{\frac{k_1+k_2}m}$.</wlatex> |
</noinclude> | </noinclude> | ||
A lap 2013. augusztus 29., 12:07-kori változata
Feladat
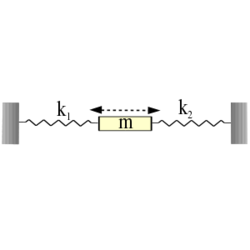
- (6.8.) Határozzuk meg a vízszintes síkon mozgó
tömegű test rezgéseinek frekvenciáját, ha az ábrán látható módon két, elhanyagolható tömegű rugóhoz van kapcsolva (rugóállandók: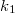 
és 
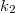)! A
Megoldás
Ha a testet kissé kimozdítjuk egyensúlyi helyzetéből, az egyik rugó húzni, a másik nyomni fogja, azaz a két rugóerő azonos írányú, így a test mozgásegyenlete![\[m\ddot x=-k_1x-k_2x,\]](/images/math/d/7/f/d7fe204fe7d9421968cb157c728fd512.png)
.
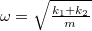