„Termodinamika példák - Gumiszalag termodinamikai potenciáljai” változatai közötti eltérés
A Fizipedia wikiből
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Gumiszalag állapotegyenlete $f=aT\left(\frac \ell{ | + | </noinclude><wlatex># Gumiszalag állapotegyenlete $f=aT\left({\textstyle \frac{\ell}{\ell_0}}-{\left({\textstyle \frac{\ell_0}{\ell}}\right)}^2\right)$ alakba írható, ahol $f$ a szalagban fellépő húzóerő nagysága, $\ell$ a szalag hossza, $T$ a hőmérséklet, $\ell_0$ a szalag erőmentes hossza, $a$ pozitív állandó.</wlatex> |
#* a) <wlatex>Mutassuk ki, hogy a belső energia nem függ a szalag hosszától!</wlatex><includeonly><wlatex>{{Útmutatás|content=A belső energia térfogatfüggésére kapott általános összefüggés átírható a vizsgált esetre a $p\to -f$ és $V\to l$ helyettesítéssel.}}</wlatex></includeonly> | #* a) <wlatex>Mutassuk ki, hogy a belső energia nem függ a szalag hosszától!</wlatex><includeonly><wlatex>{{Útmutatás|content=A belső energia térfogatfüggésére kapott általános összefüggés átírható a vizsgált esetre a $p\to -f$ és $V\to l$ helyettesítéssel.}}</wlatex></includeonly> | ||
#* b) <wlatex>Írjuk fel a termodinamika fundamentális egyenletét, továbbá a szabad energia- és a szabad entalpia megváltozását a gumiszalagra! | #* b) <wlatex>Írjuk fel a termodinamika fundamentális egyenletét, továbbá a szabad energia- és a szabad entalpia megváltozását a gumiszalagra! | ||
A lap 2013. április 16., 13:15-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Homogén rendszerek |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Gumiszalag állapotegyenlete
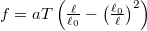alakba írható, ahol 
a szalagban fellépő húzóerő nagysága,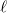 
a szalag hossza, 
a hőmérséklet, 
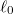a szalag erőmentes hossza, 
pozitív állandó.
- a) Mutassuk ki, hogy a belső energia nem függ a szalag hosszától!
- b) Írjuk fel a termodinamika fundamentális egyenletét, továbbá a szabad energia- és a szabad entalpia megváltozását a gumiszalagra!
- c) Mekkora munkát végzünk, és mennyi a gumiszalag által leadott hő, ha a szalag hosszát izotermikus, reverzíbilis folyamatban 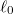-ról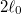
-ra növeljük.
- d) Igazoljuk, hogy a fonal hőmérséklete megnő, ha adiabatikusan megnyújtjuk!
Megoldás
Megoldás szövege
