„Termodinamika példák - Gumiszalag termodinamikai potenciáljai” változatai közötti eltérés
A Fizipedia wikiből
| 17. sor: | 17. sor: | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>'''a)''' Az [[Termodinamika példák - További differenciális összefüggések, általános változócsere|általános változócseréről]] szóló feladatban tárgyaltak szerint a belső energia térfogatfüggésére $p\to -f$ és $V\to\ell$ általános változócserével belátható: |
| + | $$ \left(\frac{\partial U}{\partial \ell}\right)_T = f - T \left(\frac{\partial f}{\partial T}\right)_\ell | ||
| + | = f - T \frac{f}{T} = 0, $$ | ||
| + | ahol a második átalakítás a kijelölt deriválás elvégzésével adódott. | ||
| + | |||
| + | '''b)''' $p\to -f$ és $V\to\ell$ általános változócserét alkalmazva | ||
| + | $$ \mathrm{d}U=T\,\mathrm{d}S+f\,\mathrm{d}\ell, $$ | ||
| + | amiből Legendre-transzformációval | ||
| + | $$ \mathrm{d}F = \mathrm{d}\left(U-TS\right) = f\,\mathrm{d}\ell-S\,\mathrm{d}T $$ | ||
| + | és | ||
| + | $$ \mathrm{d}G = \mathrm{d}\left(U-TS-fl\right) = -\ell\,\mathrm{d}f-S\,\mathrm{d}T. $$ | ||
| + | |||
| + | '''c)''' Az első főtétel értelmében | ||
| + | $$ \mathrm{d}U = \delta Q + \mathrm{d}W, $$ | ||
| + | ahol ''a)'' részben beláttuk, hogy ebben a speciális esetben a állandó hőmérsékleten $U$ nem függ a szalag hosszától, azaz $ \mathrm{d}U = 0 $: | ||
| + | $$ \delta Q= -\mathrm{d}W= - f \,\mathrm{d}\ell $$ | ||
| + | |||
| + | A nyújtás hatására ($\mathrm{d}\ell>0$) a gumiszalag hőt ad le: | ||
| + | $$ \Delta Q= -\Delta W = -\int_{\ell_0}^{2\ell_0} f\,\mathrm{d}\ell | ||
| + | = \int_{\ell_0}^{2\ell_0} aT\left( \left(\frac{\ell_0}{\ell}\right)^2-\frac{\ell}{\ell_0}\right)\,\mathrm{d}\ell | ||
| + | = aT \left(-\frac{\ell_0^2}{\ell}-\frac{\ell^2}{2 \ell_0}\right)_{\ell_0}^{2 \ell_0} = -aT \ell_0$$ | ||
| + | |||
| + | '''d)''' Az első főtétel értelmében | ||
| + | $$ \mathrm{d}U = \delta Q + \mathrm{d}W, $$ | ||
| + | ahol adiabatikus esetben $ \delta Q=0 $ | ||
| + | $$ \mathrm{d}U=f\,\mathrm{d}\ell, $$ | ||
| + | másrészt definíció szerint | ||
| + | $$ \mathrm{d}U= C_\ell\,\mathrm{d}T, $$ | ||
| + | amiből | ||
| + | $$ \left(\frac{\partial T}{\partial l}\right)_S=\frac f{C_l}. $$ | ||
| + | |||
| + | Természetesen $f>0$, $C_\ell>0$ és megnyújtáskor $\mathrm{d}\ell>0$ ezért $\mathrm{d}T>0$. | ||
| + | |||
| + | == Megjegyzés == | ||
| + | Az állandó hosszon mért fajhő definíciójához | ||
| + | $$ \mathrm{d}U = \left(\frac{\partial U}{\partial T}\right)_\ell\,\mathrm{d}T + \left(\frac{\partial U}{\partial \ell}\right)_T\,\mathrm{d}\ell $$ | ||
| + | teljes differenciálból juthatunk $\mathrm{d}\ell=0$ esetben. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 17., 19:23-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Homogén rendszerek |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Gumiszalag állapotegyenlete
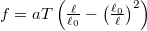 alakba írható, ahol
alakba írható, ahol  a szalagban fellépő húzóerő nagysága,
a szalagban fellépő húzóerő nagysága, 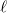 a szalag hossza,
a szalag hossza,  a hőmérséklet,
a hőmérséklet, 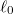 a szalag erőmentes hossza,
a szalag erőmentes hossza,  pozitív állandó.
pozitív állandó.
- a) Mutassuk ki, hogy a belső energia nem függ a szalag hosszától!
- b) Írjuk fel a termodinamika fundamentális egyenletét, továbbá a szabad energia- és a szabad entalpia megváltozását a gumiszalagra!
- c) Mekkora munkát végzünk, és mennyi a gumiszalag által leadott hő, ha a szalag hosszát izotermikus, reverzíbilis folyamatban
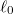 -ról
-ról 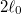 -ra növeljük.
-ra növeljük.
- d) Igazoljuk, hogy a fonal hőmérséklete megnő, ha adiabatikusan megnyújtjuk!
Megoldás
a) Az általános változócseréről szóló feladatban tárgyaltak szerint a belső energia térfogatfüggésére 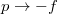 és
és 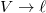 általános változócserével belátható:
általános változócserével belátható:
![\[ \left(\frac{\partial U}{\partial \ell}\right)_T = f - T \left(\frac{\partial f}{\partial T}\right)_\ell = f - T \frac{f}{T} = 0, \]](/images/math/d/1/c/d1cf26cfb6c9e3c31d9d0902ebe53a8c.png)
ahol a második átalakítás a kijelölt deriválás elvégzésével adódott.
b) 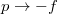 és
és 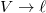 általános változócserét alkalmazva
általános változócserét alkalmazva
![\[ \mathrm{d}U=T\,\mathrm{d}S+f\,\mathrm{d}\ell, \]](/images/math/2/3/7/237fe746e99567f870b945fffe681876.png)
amiből Legendre-transzformációval
![\[ \mathrm{d}F = \mathrm{d}\left(U-TS\right) = f\,\mathrm{d}\ell-S\,\mathrm{d}T \]](/images/math/0/f/2/0f21db801559f85c1aee2984b1594742.png)
és
![\[ \mathrm{d}G = \mathrm{d}\left(U-TS-fl\right) = -\ell\,\mathrm{d}f-S\,\mathrm{d}T. \]](/images/math/9/1/a/91a52879228cd656eebd6a6c07dbfaab.png)
c) Az első főtétel értelmében
![\[ \mathrm{d}U = \delta Q + \mathrm{d}W, \]](/images/math/d/0/c/d0cc92ba83e3898764f2ed393cccbbc5.png)
ahol a) részben beláttuk, hogy ebben a speciális esetben a állandó hőmérsékleten  nem függ a szalag hosszától, azaz
nem függ a szalag hosszától, azaz 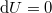 :
:
![\[ \delta Q= -\mathrm{d}W= - f \,\mathrm{d}\ell \]](/images/math/9/c/3/9c33cea4d94cd88455e5de25e156f523.png)
A nyújtás hatására (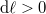 ) a gumiszalag hőt ad le:
) a gumiszalag hőt ad le:
![\[ \Delta Q= -\Delta W = -\int_{\ell_0}^{2\ell_0} f\,\mathrm{d}\ell = \int_{\ell_0}^{2\ell_0} aT\left( \left(\frac{\ell_0}{\ell}\right)^2-\frac{\ell}{\ell_0}\right)\,\mathrm{d}\ell = aT \left(-\frac{\ell_0^2}{\ell}-\frac{\ell^2}{2 \ell_0}\right)_{\ell_0}^{2 \ell_0} = -aT \ell_0\]](/images/math/9/7/d/97d7534ac8cbb479635a1b642cf1c8de.png)
d) Az első főtétel értelmében
![\[ \mathrm{d}U = \delta Q + \mathrm{d}W, \]](/images/math/d/0/c/d0cc92ba83e3898764f2ed393cccbbc5.png)
ahol adiabatikus esetben 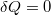
![\[ \mathrm{d}U=f\,\mathrm{d}\ell, \]](/images/math/f/9/b/f9bcba5efdadcb1e46da67c09005ec39.png)
másrészt definíció szerint
![\[ \mathrm{d}U= C_\ell\,\mathrm{d}T, \]](/images/math/3/c/7/3c7d6719b2e307bd7de8e9c4ca889347.png)
amiből
![\[ \left(\frac{\partial T}{\partial l}\right)_S=\frac f{C_l}. \]](/images/math/e/5/c/e5c46f56444212c35262c0eff53b9407.png)
Természetesen 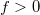 ,
, 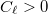 és megnyújtáskor
és megnyújtáskor 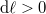 ezért
ezért  .
.
Megjegyzés
Az állandó hosszon mért fajhő definíciójához
![\[ \mathrm{d}U = \left(\frac{\partial U}{\partial T}\right)_\ell\,\mathrm{d}T + \left(\frac{\partial U}{\partial \ell}\right)_T\,\mathrm{d}\ell \]](/images/math/9/0/f/90f52eb4adf47066b556f12386bad121.png)
teljes differenciálból juthatunk 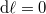 esetben.
esetben.