„Termodinamika példák - Maxwell-relációk” változatai közötti eltérés
A Fizipedia wikiből
a (Szöveg koherenssé tétele.) |
a |
||
| 10. sor: | 10. sor: | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># Bizonyítsuk be a $\displaystyle {\left(\frac{\partial p}{\partial T}\right)}_V={\left(\frac{\partial S}{\partial V}\right)}_T$ Maxwell-összefüggést!</wlatex><noinclude> | </noinclude><wlatex># Bizonyítsuk be a $\displaystyle {\left(\frac{\partial p}{\partial T}\right)}_V={\left(\frac{\partial S}{\partial V}\right)}_T$ Maxwell-összefüggést!</wlatex><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>A Maxwell-relációk a termodinamikai potenciálok kétszeres parciális deriváltjainak Young-tétel szerinti megfeleltetéséből kaphatóak. Számításainkat nem csak a feladatban előírt, hanem minden termodinamikai potenciálra elvégezzük. | <wlatex>A Maxwell-relációk a termodinamikai potenciálok kétszeres parciális deriváltjainak Young-tétel szerinti megfeleltetéséből kaphatóak. Számításainkat nem csak a feladatban előírt, hanem minden termodinamikai potenciálra elvégezzük. | ||
A lap 2013. május 20., 12:53-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Homogén rendszerek |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Bizonyítsuk be a
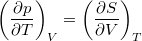Maxwell-összefüggést!
Megoldás
A Maxwell-relációk a termodinamikai potenciálok kétszeres parciális deriváltjainak Young-tétel szerinti megfeleltetéséből kaphatóak. Számításainkat nem csak a feladatban előírt, hanem minden termodinamikai potenciálra elvégezzük.
Az előző feladat alapján a termodinamika differenciális összefüggései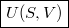 
-re:
![\[ \left(\frac{\partial U}{\partial S}\right)_V = T, \qquad \left(\frac{\partial U}{\partial V}\right)_S = -p. \]](/images/math/6/3/7/637765774817409b7e8a6d08614d94f1.png)
A Young-tétel értelmében
![\[ \frac{\partial}{\partial V}\left(\frac{\partial U}{\partial S}\right)_V = \frac{\partial}{\partial S}\left(\frac{\partial U}{\partial V}\right)_S, \]](/images/math/2/1/7/217ac46bda137e26dc37e0cf926aedd3.png)
azaz
![\[ \left(\frac{\partial T}{\partial V}\right)_S = -\left(\frac{\partial p}{\partial S}\right)_V. \]](/images/math/c/c/6/cc6b94115b5aa35898d60f3f3bec57e6.png)
Az előző feladat alapján a termodinamika differenciális összefüggései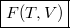 
-re:
![\[ \left(\frac{\partial F}{\partial T}\right)_V = -S, \qquad \left(\frac{\partial F}{\partial V}\right)_T = -p. \]](/images/math/0/7/0/0706881a87c9005b38dded32357e5366.png)
A Young-tétel értelmében
![\[ \frac{\partial}{\partial T}\left(\frac{\partial F}{\partial V}\right)_T = \frac{\partial}{\partial V}\left(\frac{\partial F}{\partial T}\right)_V, \]](/images/math/9/0/0/900f87d9d1da291a33315b31c9819007.png)
azaz
![\[ \left(\frac{\partial p}{\partial T}\right)_V = \left(\frac{\partial S}{\partial V}\right)_T \]](/images/math/b/0/1/b01a639d08f8e8afb6543ba329d6b655.png)
a keresett összefüggés.
Hasonlóan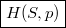 
-re
![\[ \left(\frac{\partial H}{\partial S}\right)_p = T, \qquad \left(\frac{\partial H}{\partial p}\right)_S = V. \]](/images/math/d/9/5/d9531493a9cdf34987675483d1bf16fc.png)
Innen
![\[ \left(\frac{\partial T}{\partial p}\right)_S = \left(\frac{\partial V}{\partial S}\right)_p, \]](/images/math/2/0/6/20618af58ec33539b5922706e3e07138.png)
ami a keresett összefüggés reciprokára hasonlít, de vegyük észre, hogy a rögzített változók mások.
Analóg módon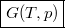 
-re
![\[ \left(\frac{\partial G}{\partial T}\right)_p = -S, \qquad \left(\frac{\partial G}{\partial p}\right)_T = V. \]](/images/math/8/b/0/8b0717f22232d1e2368097060b2d250b.png)
Innen
![\[ -\left(\frac{\partial S}{\partial p}\right)_T = \left(\frac{\partial V}{\partial T}\right)_p. \]](/images/math/8/e/2/8e2b2432a9422b5b96822ed732086e23.png)
