Termodinamika példák - Átadott hő mérhető mennyiségekkel

Feladat

1. Feltételezve, hogy 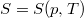$\setbox0\hbox{$S=S(p,T)$}% \message{//depth:\the\dp0//}% \box0%$, mutassuk ki, hogy 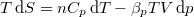$\setbox0\hbox{$T\,\mathrm{d}S=n C_p\,\mathrm{d}T-\beta_p TV\,\mathrm{d}p$}% \message{//depth:\the\dp0//}% \box0%$, ahol 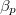$\setbox0\hbox{$\beta_p$}% \message{//depth:\the\dp0//}% \box0%$ az izobár hőtágulási együttható.

Megoldás

Írjuk fel 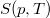$\setbox0\hbox{$S(p,T)$}% \message{//depth:\the\dp0//}% \box0%$ teljes differenciálját

$\[ \mathrm{d}S = \left(\frac{\partial S}{\partial p}\right)_T\,\mathrm{d}p + \left(\frac{\partial S}{\partial T}\right)_p\,\mathrm{d}T, \]$

és az első tagban használjuk a Maxwell-féle összefüggést és a kompresszibilitás definícióját:

$\[ \left(\frac{\partial S}{\partial p}\right)_T = -\left(\frac{\partial V}{\partial T}\right)_p = -V \beta_p. \]$

A másodikra tagban alkalmazzuk a láncszabályt (ehhez minden differenciálhányadost ugyanazon rögzített változó mellett kell felírni) és a fajhő definícióját:

$\[ \left(\frac{\partial S}{\partial T}\right)_p \left(\frac{\partial H}{\partial H}\right)_p = \left(\frac{\partial S}{\partial H}\right)_p \left(\frac{\partial H}{\partial T}\right)_p = \left(\frac{\partial S}{\partial H}\right)_p n C_p, \]$

aminek továbbalakításához használjuk a 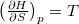$\setbox0\hbox{$\left(\frac{\partial H}{\partial S}\right)_p=T$}% \message{//depth:\the\dp0//}% \box0%$ differenciális összefüggés reciprokát, így az entrópia megváltozása

$\[ \mathrm{d}S = -V \beta_p\,\mathrm{d}p + \frac{n C_p}{T}\,\mathrm{d}T. \]$

$\setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0%$-vel való szorzás után

$\[ T\,\mathrm{d}S = -\beta_p T V\,\mathrm{d}p+ n C_p\,\mathrm{d}T \]$

eredmény már adódik.