Magnetosztatika - Erőhatások mágneses térben
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Beleznai (vitalap | szerkesztései) 2013. július 1., 08:44-kor történt szerkesztése után volt.
Feladatok
- Egy
 oldalú négyzet csúcspontjaiba egyforma
oldalú négyzet csúcspontjaiba egyforma 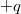 töltést helyezünk.Mekkora és milyen irányú erő hat egy-egy töltésre? Hova kellene helyezni egy újabb töltést, hogy egyikre se hasson erő? Mekkora nagyságú, és milyen előjelű ez a töltés?
töltést helyezünk.Mekkora és milyen irányú erő hat egy-egy töltésre? Hova kellene helyezni egy újabb töltést, hogy egyikre se hasson erő? Mekkora nagyságú, és milyen előjelű ez a töltés?
- Egy
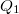 és egy
és egy 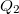 nagyságú pontszerű töltés
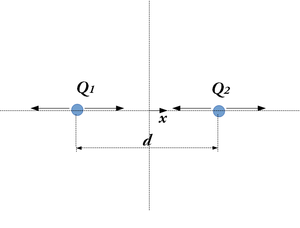
nagyságú pontszerű töltés  távolságra helyezkedik el egymástól. Határozzuk meg a töltéserendezés terének térerősségét, a két töltést összekötő egyenes mentén a töltések közötti távolság felezőpontjából mért távolság függvényében!
távolságra helyezkedik el egymástól. Határozzuk meg a töltéserendezés terének térerősségét, a két töltést összekötő egyenes mentén a töltések közötti távolság felezőpontjából mért távolság függvényében!
- Egy
 sugarú vékony körvezető töltése
sugarú vékony körvezető töltése  . Határozzuk meg a térerősséget a körvezető tengelyén, a körvezető síkjától
. Határozzuk meg a térerősséget a körvezető tengelyén, a körvezető síkjától  távolságban. A tengely mely pontján a legnagyobb a térerősség?
távolságban. A tengely mely pontján a legnagyobb a térerősség?
- Adott egy
 sugarú korong egyenletesen töltött
sugarú korong egyenletesen töltött  felületi töltéssűrűséggel. Határozzuk meg a térerősséget a körvezető tengelyén, a korong síkjától
felületi töltéssűrűséggel. Határozzuk meg a térerősséget a körvezető tengelyén, a korong síkjától  távolságban!
távolságban!
- Végtelen hosszú egyenes fonálon a lineáris töltéssűrűség
 . Mekkora az elektromos térerősség a fonáltól
. Mekkora az elektromos térerősség a fonáltól  távolságra? ( A keresett térerősséget, pontszerű töltések erőterének szuperpozíciójaként állítsuk elő!)
távolságra? ( A keresett térerősséget, pontszerű töltések erőterének szuperpozíciójaként állítsuk elő!)
- Végtelen hosszú egyenes fonálon a lineáris töltéssűrűség
 . Határozzuk meg a térerősséget a fonáltól
. Határozzuk meg a térerősséget a fonáltól  távolságra a Gauss-tétel segítségével!
távolságra a Gauss-tétel segítségével!
- Végtelen kiterjedésű síkon
 felületi töltéssűrűség van. Határozzuk meg a térerősséget a Gauss-tétel segítségével a síktól
felületi töltéssűrűség van. Határozzuk meg a térerősséget a Gauss-tétel segítségével a síktól  távolságra!
távolságra!
- Milyen erőteret hoz létre két, egymásra merőleges végtelen sík, ha rajtuk egyenletesen elosztva
 és
és 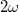 töltéssűrűség van?
töltéssűrűség van?
- Egy
 sugarú gömbben egyenletes
sugarú gömbben egyenletes  térfogati töltéssűrűség van. Határozzuk meg a térerősséget a gömb középpontjától mért távolság függvényében, a gömbön belül és kívül!
térfogati töltéssűrűség van. Határozzuk meg a térerősséget a gömb középpontjától mért távolság függvényében, a gömbön belül és kívül!
- Egy
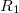 sugarú gömben egyenletes
sugarú gömben egyenletes  térfogati töltéssűrűség van. Ezt egy
térfogati töltéssűrűség van. Ezt egy 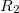 sugarú földelt fémgömb veszi körül koncentrikus elrendezésben.
sugarú földelt fémgömb veszi körül koncentrikus elrendezésben.
a) Határozzuk meg, a térerősséget a gömb középpontjától mért távolság függvényében, a gömbön belül és kívül!
b) Mekkora felületi töltéssűrűség alakul ki a földelt gömbhéj belső felületén?
- Egy állandó
 térfogati töltéssűrűségű
térfogati töltéssűrűségű  sugarú gömben a közzéppontól
sugarú gömben a közzéppontól  távolságra egy
távolságra egy  sugarú üreg van (
sugarú üreg van (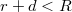 ). Mekkora a térerősség az üregben?
). Mekkora a térerősség az üregben?
- Egymástól
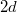 távolságban párhuzamosan elhelyezett két igen hosszú fonalat egyenletesen töltünk fel
távolságban párhuzamosan elhelyezett két igen hosszú fonalat egyenletesen töltünk fel 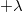 és
és 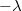 lineáris töltéssűrűséggel. Határozzuk meg a térerősséget abban a pontban, mely a két fonalat magában foglaló síktól
lineáris töltéssűrűséggel. Határozzuk meg a térerősséget abban a pontban, mely a két fonalat magában foglaló síktól  távolságban helyezkedik el a rendszer szimmetriasíkjában!
távolságban helyezkedik el a rendszer szimmetriasíkjában!
- Egy vékony szigetelő drótot
 sugarú kör alakúra hajlítunk, és
sugarú kör alakúra hajlítunk, és 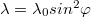 lineáris töltéssűrűséggel látunk el, ahol
lineáris töltéssűrűséggel látunk el, ahol  a drót kezdőpontja és az aktuális hely közötti középponti szög. Határozzuk meg, és ábrázoljuk a térerősséget a kör tengelyén a kör síkjától mért
a drót kezdőpontja és az aktuális hely közötti középponti szög. Határozzuk meg, és ábrázoljuk a térerősséget a kör tengelyén a kör síkjától mért  távolság függvényében!
távolság függvényében!
 sugarú szigetelő gömb térfogatában
sugarú szigetelő gömb térfogatában  töltés oszlik el egyenletesen. A gömböt egy véges vastagságú fém gömbhéj veszi körül, melynek görbületi sugarai
töltés oszlik el egyenletesen. A gömböt egy véges vastagságú fém gömbhéj veszi körül, melynek görbületi sugarai  és
és 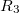 . A gömbhéj eredő töltése 0.
. A gömbhéj eredő töltése 0.
a) Határozzuk meg a szigetelő gömbben a térfogati töltéssűrűséget!
b) Milyen előjelű és milyen nagyságú felületi töltéssűrűség alakul ki az és
és 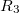 sugarú felületeken?
sugarú felületeken?
c) Határozzuk meg a térerősséget az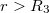 sugáron!
sugáron!
d) Rajzoljuk fel jellegre helyesen az elektromos térerősséget, mint a távolság függvényét!
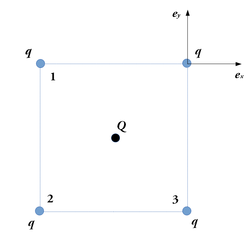
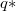 ellentétes előjelű töltést tennünk, ahol
ellentétes előjelű töltést tennünk, ahol 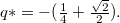
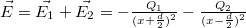
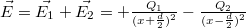
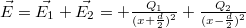
![\[ z=\dfrac{r}{\sqrt{2}}\]](/images/math/8/2/5/82567e131eb8f6e89cf20bf7109cac64.png)
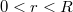 sugarú töltött gyűrűk sokaságára
sugarú töltött gyűrűk sokaságára ![\[E=\dfrac{\omega}{2\varepsilon_{0}} \left(1-\dfrac{z}{(R^2+z^2)^{1/2}} \right)\]](/images/math/e/7/6/e760b68831c68f2b1ca6a11b95ddee89.png)
![\[\vec{E_{z}} = \frac{2\cdot k\cdot\lambda}{d}\]](/images/math/0/a/3/0a330317445f95b81ca8ec5dbbd30fe6.png)
![\[\vec{E}= \frac{\lambda}{2\cdot r\cdot\epsilon_{0}\cdot\pi}\]](/images/math/6/0/4/604861a9e23b3498d3e96a961e6cc21b.png)
![\[E=\dfrac{\omega}{2\varepsilon_0} \]](/images/math/e/2/6/e26be922b627f50e8d32ed593468c2e1.png)
![\[\overline{E}=\dfrac{\omega}{\varepsilon_0}\left( \dfrac{x}{\vert x\vert}\overline{i}+\dfrac{y}{2\vert y\vert}\overline{j} \right)\]](/images/math/8/5/0/85031d55794ce0f5acd93534b092d91f.png)
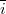 és
és 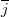 az
az  és
és  irányú egységvektorok.
irányú egységvektorok. ![\[\vec{E}=\frac{\rho\cdot r}{\epsilon_{0}\cdot 3}\cdot\vec{e_{r}}\]](/images/math/e/3/0/e30aec9803d933b7acabfb8843f72edb.png)
![\[\vec{E}=\frac{\rho\cdot R^{3}}{\epsilon_{0}\cdot 3\cdot r^{2}}\cdot\vec{e_{r}}\]](/images/math/5/6/e/56e41121a5ed4c2cd4e68dbe29bfdc7a.png)
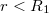 :
: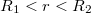 ::
:: 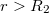 :
: ![\[\vec{E}=0\]](/images/math/2/c/d/2cd8159c5107d7b441bcba4a41bb2ea1.png)
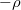 töltéssűrűségű
töltéssűrűségű ![\[\vec{E}=\frac{\pi\cdot\rho}{3\cdot\epsilon_{0}}\cdot\vec{d}\]](/images/math/f/e/e/feef12b2a50099ef8ae11b686d0fec6d.png)
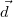 az origóból az üreg közepébe mutató vektor.
az origóból az üreg közepébe mutató vektor. ![\[ E_e=\dfrac{\lambda}{\pi\varepsilon_0}\dfrac{d}{(d^2+z^2)}\]](/images/math/9/c/0/9c0c16af5ed3b4ee67e6c1206b32a413.png)
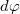 szög alatt látszó ívelemekre bontjuk, és a kérdéses pontban összegezzük a gyűrűelemek térerősség járulékait.
szög alatt látszó ívelemekre bontjuk, és a kérdéses pontban összegezzük a gyűrűelemek térerősség járulékait. ![\[E=\dfrac{\lambda_0 R}{4\varepsilon_{0}}\dfrac{z}{(R^2+z^2)^{3/2}}\]](/images/math/6/7/3/673a6c7af6055806a6e118a141b28be8.png)
![\[\varrho=\dfrac{Q}{\dfrac{4}{3}R_1^3\pi}\]](/images/math/a/5/a/a5a8d64357cbc4cd512ed3de0c3c745c.png)
![\[\omega_2=\dfrac{-Q}{4R_2^2\pi}\]](/images/math/1/0/b/10b0257aecae9a1ef85eb9a6162234d5.png)
![\[\omega_3=\dfrac{Q}{4R_3^2\pi}\]](/images/math/0/4/b/04b60fad70a1ad31c4d6ebe370f24148.png)
![\[E=\dfrac{1}{4\pi\varepsilon_0}\dfrac{Q}{r^2}\]](/images/math/c/0/7/c0711a67bf70979b3d447ad9c873f80b.png)