Termodinamika példák - További differenciális összefüggések, általános változócsere

Feladat

1. Állandó anyagmennyiségű homogén rendszerben termikus és mechanikai kölcsönhatás esetén fennáll a 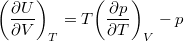$\setbox0\hbox{$\displaystyle {\left(\frac{\partial U}{\partial V}\right)}_T=T{\left(\frac{\partial p}{\partial T}\right)}_V-p$}% \message{//depth:\the\dp0//}% \box0%$ egyenlet. A fenti egyenlet levezetésének mintájára bizonyítsuk be, hogy ha a termikus kölcsönhatás mellett tetszőleges – 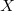$\setbox0\hbox{$X$}% \message{//depth:\the\dp0//}% \box0%$ intenzív- és 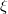$\setbox0\hbox{$\xi$}% \message{//depth:\the\dp0//}% \box0%$ extenzív mennyiségpárral jellemzett – kölcsönhatás lép fel, akkor a fenti egyenlet érvényes marad, ha végrehajtjuk a 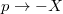$\setbox0\hbox{$p\to-X$}% \message{//depth:\the\dp0//}% \box0%$ és a $\setbox0\hbox{$V\to\xi$}% \message{//depth:\the\dp0//}% \box0%$ 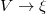változócserét!

Megoldás

Az első főtétel az új változókkal

$\[ T\,\mathrm{d}S=\,\mathrm{d}U-X\,\mathrm{d}\xi. \]$

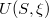Az $\setbox0\hbox{$U(S,\xi)$}% \message{//depth:\the\dp0//}% \box0%$ függvény teljes differenciálja

$\[ \mathrm{d}U = \left(\frac{\partial U}{\partial T}\right)_\xi \,\mathrm{d}T + \left(\frac{\partial U}{\partial \xi}\right)_T \,\mathrm{d}\xi, \]$

aminek segítségével

$\[ \mathrm{d}S = \frac{1}{T} \left(\frac{\partial U}{\partial T}\right)_\xi \,\mathrm{d}T + \frac{1}{T} \left( \left(\frac{\partial U}{\partial \xi}\right)_T - X \right) \,\mathrm{d}\xi. \]$

A Young-tétel szerint 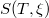$\setbox0\hbox{$S(T,\xi)$}% \message{//depth:\the\dp0//}% \box0%$ vegyes második parciális deriváltjai egyenlőek:

$\[ \frac{\partial}{\partial \xi} \left(\frac{1}{T} \left(\frac{\partial U}{\partial T}\right)_\xi \right) = \frac{\partial}{\partial T} \left(\frac{1}{T} \left(\frac{\partial U}{\partial \xi}\right)_T - \frac{X}{T} \right), \]$

$\[ \frac{1}{T} \frac{\partial^2 U}{\partial \xi \partial T} = -\frac{1}{T^2}\frac{\partial U}{\partial \xi} + \frac{1}{T} \frac{\partial^2 U}{\partial \xi \partial T} -\frac{1}{T} \frac{\partial X}{\partial T} + \frac{X}{T^2}, \]$

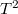azaz $\setbox0\hbox{$T^2$}% \message{//depth:\the\dp0//}% \box0%$-tel való szorzás után

$\[ \left(\frac{\partial U}{\partial \xi }\right)_T = X - T \left(\frac{\partial X}{\partial T}\right)_\xi. \]$

Természetesen a levezetés 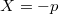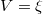$\setbox0\hbox{$X=-p$}% \message{//depth:\the\dp0//}% \box0%$, $\setbox0\hbox{$V=\xi$}% \message{//depth:\the\dp0//}% \box0%$ esetben is igaz.

Másik bizonyítás

Az első főtétel az új változókkal

$\[ \mathrm{d}U = T\,\mathrm{d}S + X\,\mathrm{d}\xi \]$

felírt alakját osszuk le formálisan 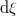$\setbox0\hbox{$\mathrm{d}\xi$}% \message{//depth:\the\dp0//}% \box0%$-vel állandó hőmérsékleten:

$\[ \left(\frac{\partial U}{\partial \xi}\right)_T = T \left(\frac{\partial S}{\partial \xi}\right)_T + X, \]$

ahol használjuk az új változókban 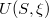$\setbox0\hbox{$U(S,\xi)$}% \message{//depth:\the\dp0//}% \box0%$ teljes differenciálból levezethető

$\[ \left(\frac{\partial S}{\partial \xi}\right)_T = -\left(\frac{\partial X}{\partial T}\right)_\xi \]$

Maxwell-relációt:

$\[ \left(\frac{\partial U}{\partial \xi }\right)_T = X - T \left(\frac{\partial X}{\partial T}\right)_\xi. \]$

Természetesen a levezetés 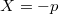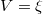$\setbox0\hbox{$X=-p$}% \message{//depth:\the\dp0//}% \box0%$, $\setbox0\hbox{$V=\xi$}% \message{//depth:\the\dp0//}% \box0%$ esetben is igaz.