Termodinamika - Homogén rendszerek
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Homogén rendszerek |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Mérhető mennyiségek
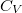 |
= | 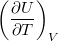
|
állandó térfogaton mért hőkapacitás* |
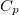 |
= | 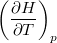
|
állandó nyomáson mért hőkapacitás* |
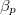 |
= | 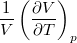
|
izobár hőtágulási együttható |
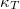 |
= | 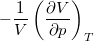
|
izoterm kompresszibilitás |
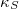 |
= | 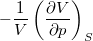
|
adiabatikus kompresszibilitás |
* ha egységnyi tömegre illetve anyagmennyiségre vonatkoztatjuk, akkor rendre fajhőnek illetve mólhőnek nevezzük.
Feladatok
- Bizonyítsuk be a
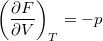 ,
, 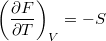 ,
, 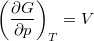 és
és 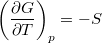 összefüggéseket!
összefüggéseket!
- Bizonyítsuk be a
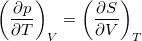 Maxwell-összefüggést!
Maxwell-összefüggést!
- Állandó anyagmennyiségű homogén rendszerben termikus és mechanikai kölcsönhatás esetén fennáll a
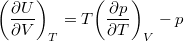 egyenlet. A fenti egyenlet levezetésének mintájára bizonyítsuk be, hogy ha a termikus kölcsönhatás mellett tetszőleges –
egyenlet. A fenti egyenlet levezetésének mintájára bizonyítsuk be, hogy ha a termikus kölcsönhatás mellett tetszőleges – 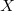 intenzív- és
intenzív- és 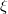 extenzív mennyiségpárral jellemzett – kölcsönhatás lép fel, akkor a fenti egyenlet érvényes marad, ha végrehajtjuk a
extenzív mennyiségpárral jellemzett – kölcsönhatás lép fel, akkor a fenti egyenlet érvényes marad, ha végrehajtjuk a 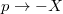 és a
és a 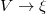 változócserét!
változócserét!
- Fejezzük ki mérhető mennyiségekkel (hőtágulási együttható, kompresszibilitás, mólhő) egy rendszer
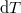 hőmérséklet-változását, ha térfogata adiabatikus, kvázisztatikus folyamat során
hőmérséklet-változását, ha térfogata adiabatikus, kvázisztatikus folyamat során 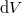 -vel megváltozik! Mutassuk meg, hogy
-vel megváltozik! Mutassuk meg, hogy 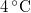 alatt a víz adiabatikus, kvázisztatikus összenyomáskor lehűl!
alatt a víz adiabatikus, kvázisztatikus összenyomáskor lehűl!
- Feltételezve, hogy
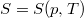 , mutassuk ki, hogy
, mutassuk ki, hogy 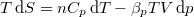 , ahol
, ahol 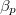 az izobár hőtágulási együttható.
az izobár hőtágulási együttható.
- Az első főtétel és a termodinamika differenciálegyenletei felhasználásával mutassuk meg, hogy ha ismerjük egy állandó anyagmennyiségű rendszer belső energiáját a térfogat és az entrópia függvényeként (vagyis az
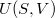 függvényt), akkor a rendszer bármely állapotjelzője (nyomás, hőmérséklet, entalpia, stb.) megadható
függvényt), akkor a rendszer bármely állapotjelzője (nyomás, hőmérséklet, entalpia, stb.) megadható  és
és  függvényeként!
függvényeként!
- Mennyivel változik egy
 tömegű,
tömegű,  hőmérsékletű,
hőmérsékletű,  térfogatú rendszer entrópiája, ha térfogata állandó nyomáson
térfogatú rendszer entrópiája, ha térfogata állandó nyomáson 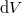 értékkel megnő? Az állandó nyomáson mért
értékkel megnő? Az állandó nyomáson mért 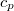 fajhőt és a
fajhőt és a 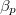 hőtágulási együtthatót ismertnek tekintjük.
hőtágulási együtthatót ismertnek tekintjük.
- Egy rendszer állapotegyenlete
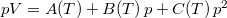 , ahol a hőmérsékletfüggő együtthatók kísérletekből ismertek. Mennyit változik a rendszer szabad entalpiája és entrópiája, ha a nyomást rögzített
, ahol a hőmérsékletfüggő együtthatók kísérletekből ismertek. Mennyit változik a rendszer szabad entalpiája és entrópiája, ha a nyomást rögzített  hőmérsékleten
hőmérsékleten 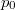 -ról
-ról 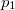 -re változtatjuk?
-re változtatjuk?
- Egy gumiszalag állapotegyenlete
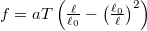 alakba írható, ahol
alakba írható, ahol  a szalagban fellépő húzóerő nagysága,
a szalagban fellépő húzóerő nagysága, 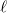 a szalag hossza,
a szalag hossza,  a hőmérséklet,
a hőmérséklet, 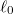 a szalag erőmentes hossza,
a szalag erőmentes hossza,  pozitív állandó.
pozitív állandó.
- a) Mutassuk ki, hogy a belső energia nem függ a szalag hosszától!
- b) Írjuk fel a termodinamika fundamentális egyenletét, továbbá a szabad energia és a szabad entalpia megváltozását a gumiszalagra!
- c) Mekkora munkát végzünk, és mennyi a gumiszalag által leadott hő, ha a szalag hosszát izotermikus, reverzíbilis folyamatban
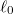 -ról
-ról 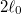 -ra növeljük.
-ra növeljük.
- d) Igazoljuk, hogy a gumiszalag hőmérséklete megnő, ha adiabatikusan megnyújtjuk!
- Mennyi hő szabadul fel az
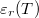 dielektromos állandójú dielektrikum polarizációjakor, ha a külső elektromos tér nagyságát állandó hőmérsékleten, kvázi-stacionáriusan növeljük nulláról egy nem túl nagy
dielektromos állandójú dielektrikum polarizációjakor, ha a külső elektromos tér nagyságát állandó hőmérsékleten, kvázi-stacionáriusan növeljük nulláról egy nem túl nagy  értékre? A térfogatváltozás elhanyagolható.
értékre? A térfogatváltozás elhanyagolható.
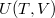 függvény teljes differenciálját, alkalmazzuk a belső energia térfogatfüggésére érvényes összefüggést, és a
függvény teljes differenciálját, alkalmazzuk a belső energia térfogatfüggésére érvényes összefüggést, és a 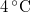 alatt negatív.
alatt negatív. 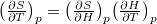 matematikai összefüggést, a termodinamika két differenciális összefüggését és a
matematikai összefüggést, a termodinamika két differenciális összefüggését és a ![\[\mathrm{d}S=\frac{m c_p}{TV\beta_p}\,\mathrm{d}V\]](/images/math/8/9/1/8913482ffd0e5fd05a97ff4d3c990a0a.png)
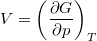 és az
és az 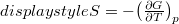 összefüggéseket!
összefüggéseket! ![\[\Delta G=A\ln\left(\frac{p_1}{p_0}\right)+B\left(p_1-p_0\right)+C\frac{p_1^2-p_0^2}{2}\]](/images/math/6/0/4/604b4690f62d9f0616982b2cd9d8dfe5.png)
![\[\Delta S=A'\ln\left(\frac{p_1}{p_0}\right)+B'\left(p_1-p_0\right)+C'\frac{p_1^2-p_0^2}{2},\]](/images/math/9/4/d/94dc473377e76fb6ed5fbb18beabd15f.png)
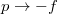 és
és 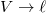 helyettesítéssel.
helyettesítéssel. ![\[\mathrm{d}U=T\mathrm{d}S+f\mathrm{d}\ell\]](/images/math/7/f/5/7f5decf22c82e848373c1a93e96bafaf.png)
![\[W=Q_\text{le}=\int_{\ell_0}^{2\ell_0}f\mathrm{d}\ell\]](/images/math/a/9/2/a92623436a83ffbf664f8f1a1b3458ef.png)
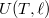 függvény teljes differenciálját, és vegyük figyelembe az (a) részfeladat eredményét!
függvény teljes differenciálját, és vegyük figyelembe az (a) részfeladat eredményét! ![\[\left(\frac{\partial T}{\partial \ell}\right)_S=\frac{f}{C_\ell}>0,\]](/images/math/4/8/f/48fb10b34970193d78d5a4a66ee9c31c.png)
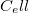 az állandó hossznál mért hőkapacitás.
az állandó hossznál mért hőkapacitás. 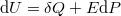 alakját, az
alakját, az 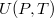 függvény teljes differenciálját, és azt, hogy a belső energia térfogatfüggésére kapott általános összefüggés átírható erre az esetre is a dielektrikum teljes dipólusmomentuma (
függvény teljes differenciálját, és azt, hogy a belső energia térfogatfüggésére kapott általános összefüggés átírható erre az esetre is a dielektrikum teljes dipólusmomentuma ( ) segítségével a
) segítségével a  és
és  helyettesítéssel:
helyettesítéssel: 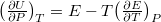 . Alkalmazzuk még a
. Alkalmazzuk még a 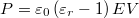 összefüggést is!
összefüggést is! ![\[Q=-\frac12T\varepsilon_0V\frac{\mathrm{d}\varepsilon_r(T)}{\mathrm{d}T}E^2\]](/images/math/7/4/8/748a2556baf501bef94eaf7c54b03a77.png)