Termodinamika példák - Entrópiaváltozás izobár táguláskor mérhető mennyiségekkel
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Homogén rendszerek |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Mennyivel változik egy
 tömegű,
tömegű,  hőmérsékletű,
hőmérsékletű,  térfogatú rendszer entrópiája, ha térfogata állandó nyomáson
térfogatú rendszer entrópiája, ha térfogata állandó nyomáson 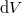 értékkel megnő? Az állandó nyomáson mért
értékkel megnő? Az állandó nyomáson mért 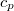 fajhőt és a
fajhőt és a 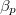 hőtágulási együtthatót ismertnek tekintjük.
hőtágulási együtthatót ismertnek tekintjük.
Megoldás
Az átadott hőt kétféle módon (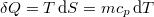 ) jellemezve jutunk
) jellemezve jutunk 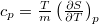 fajhődefinícióhoz.
Az
fajhődefinícióhoz.
Az 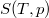 teljes differenciálja
teljes differenciálja
![\[ \mathrm{d}S = \left(\frac{\partial S}{\partial T}\right)_p \mathrm{d}T + \left(\frac{\partial S}{\partial p}\right)_T \mathrm{d}p, \]](/images/math/2/0/a/20a6cd9d8f81155c4313d00e7ff0ae4b.png)
amit állandó nyomáson bővítünk:
![\[ \mathrm{d}S = \left(\frac{\partial S}{\partial T}\right)_p \mathrm{d}T = \frac{m c_p} T\,\mathrm{d}T\frac{\,\mathrm{d}V}{\,\mathrm{d}V} = \frac{m c_p} T\left(\frac{\partial T}{\partial V}\right)_p \mathrm{d}V = \frac{m c_p}{TV \beta_p}\,\mathrm{d}V. \]](/images/math/6/a/c/6ac216b6dd03cfe7b05083bb4dbf3b83.png)