„Termodinamika példák - Állapotjelzők a térfogat és az entrópia függvényeként” változatai közötti eltérés
A Fizipedia wikiből
a (Szöveg koherenssé tétele) |
|||
| 10. sor: | 10. sor: | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># Az első főtétel és a termodinamika differenciálegyenletei felhasználásával mutassuk meg, hogy ha ismerjük egy állandó anyagmennyiségű rendszer belső energiáját a térfogat és az entrópia függvényeként (vagyis az $U(S, V)$ függvényt), akkor a rendszer bármely állapotjelzője (nyomás, hőmérséklet, entalpia, stb.) megadható $S$ és $V$ függvényeként!</wlatex><noinclude> | </noinclude><wlatex># Az első főtétel és a termodinamika differenciálegyenletei felhasználásával mutassuk meg, hogy ha ismerjük egy állandó anyagmennyiségű rendszer belső energiáját a térfogat és az entrópia függvényeként (vagyis az $U(S, V)$ függvényt), akkor a rendszer bármely állapotjelzője (nyomás, hőmérséklet, entalpia, stb.) megadható $S$ és $V$ függvényeként!</wlatex><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>Először azt látjuk be, hogy minden állapotjelző megadható a belső energiával és természetes változóival. Az első főtételből | <wlatex>Először azt látjuk be, hogy minden állapotjelző megadható a belső energiával és természetes változóival. Az első főtételből | ||
| 16. sor: | 17. sor: | ||
$$ \mathrm{d}U={\left(\frac{\partial U}{\partial S}\right)}_V\,\mathrm{d}S+{\left(\frac{\partial U}{\partial V}\right)}_S\,\mathrm{d}V$$ | $$ \mathrm{d}U={\left(\frac{\partial U}{\partial S}\right)}_V\,\mathrm{d}S+{\left(\frac{\partial U}{\partial V}\right)}_S\,\mathrm{d}V$$ | ||
beazonosíthatjuk a két hiányzó állapotjelzőt: | beazonosíthatjuk a két hiányzó állapotjelzőt: | ||
| − | $$ \left(\frac{\partial U}{\partial S}\right)_V=T, \qquad \left(\frac{\partial U}{\partial V}\right)_S=-p $$ | + | $$ \left(\frac{\partial U}{\partial S}\right)_V=T, \qquad \left(\frac{\partial U}{\partial V}\right)_S=-p. $$ |
Ezek után változócserével (Legendre-transzformációval) juthatunk a többi termodinamikai potenciálhoz: | Ezek után változócserével (Legendre-transzformációval) juthatunk a többi termodinamikai potenciálhoz: | ||
| 23. sor: | 24. sor: | ||
és | és | ||
$$ G=U+pV-TS=U-\left(\frac{\partial U}{\partial V}\right)_S V - \left(\frac{\partial U}{\partial S}\right)_V S. $$ | $$ G=U+pV-TS=U-\left(\frac{\partial U}{\partial V}\right)_S V - \left(\frac{\partial U}{\partial S}\right)_V S. $$ | ||
| + | |||
== Megjegyzés == | == Megjegyzés == | ||
| − | Ezeket a számításokat a [[Termodinamika példák - A termodinamika differenciális összefüggései|termodinamika differenciális összefüggéseiről]] szóló feladatban már elvégeztük, és ott adtunk utalást a kémiai potenciál kezelésére is, | + | Ezeket a számításokat a [[Termodinamika példák - A termodinamika differenciális összefüggései|termodinamika differenciális összefüggéseiről]] szóló feladatban már elvégeztük, és ott adtunk utalást a kémiai potenciál kezelésére is. A feladatot $U(S,V,N)$ háromváltozós függvényre |
| + | $$ \mathrm{d}U=T\,\mathrm{d}S-p\,\mathrm{d}V+\mu\,\mathrm{d}N $$ | ||
| + | összefüggéssel egészíthetjük ki, a megoldás alakjának értelmezésében pedig az említett feladatban nyert $\mu = \left(\frac{\partial U}{\partial N}\right)_{S,V}$ és $\mu = \frac{G(T,p)}{N}$ észrevétel segít. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. május 24., 18:56-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Homogén rendszerek |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Az első főtétel és a termodinamika differenciálegyenletei felhasználásával mutassuk meg, hogy ha ismerjük egy állandó anyagmennyiségű rendszer belső energiáját a térfogat és az entrópia függvényeként (vagyis az
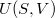függvényt), akkor a rendszer bármely állapotjelzője (nyomás, hőmérséklet, entalpia, stb.) megadható 
és 
függvényeként!
Megoldás
Először azt látjuk be, hogy minden állapotjelző megadható a belső energiával és természetes változóival. Az első főtételből
![\[ \mathrm{d}U=T\,\mathrm{d}S-p\,\mathrm{d}V \]](/images/math/6/2/0/620d8d0470dd0f29c77c59bbfc35819e.png)
és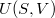 
teljes differenciáljából
![\[ \mathrm{d}U={\left(\frac{\partial U}{\partial S}\right)}_V\,\mathrm{d}S+{\left(\frac{\partial U}{\partial V}\right)}_S\,\mathrm{d}V\]](/images/math/9/7/0/9705fd8518d4f0dfaf31847809db246a.png)
beazonosíthatjuk a két hiányzó állapotjelzőt:
![\[ \left(\frac{\partial U}{\partial S}\right)_V=T, \qquad \left(\frac{\partial U}{\partial V}\right)_S=-p. \]](/images/math/3/7/e/37eea78200c9efd4645e2f4cd4a00c4c.png)
Ezek után változócserével (Legendre-transzformációval) juthatunk a többi termodinamikai potenciálhoz:
![\[ H=U+pV=U-\left(\frac{\partial U}{\partial V}\right)_S V, \]](/images/math/c/f/4/cf4cdd744df9b1c011af6143eb0872be.png)
![\[ F=U-TS=U-\left(\frac{\partial U}{\partial S}\right)_V S \]](/images/math/2/e/3/2e34a97416e764cc35569a0cc2ea2806.png)
és
![\[ G=U+pV-TS=U-\left(\frac{\partial U}{\partial V}\right)_S V - \left(\frac{\partial U}{\partial S}\right)_V S. \]](/images/math/c/c/2/cc225d1562bf41d2d81156f2d6c4b4b0.png)
Megjegyzés
Ezeket a számításokat a termodinamika differenciális összefüggéseiről szóló feladatban már elvégeztük, és ott adtunk utalást a kémiai potenciál kezelésére is. A feladatot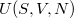 
háromváltozós függvényre
![\[ \mathrm{d}U=T\,\mathrm{d}S-p\,\mathrm{d}V+\mu\,\mathrm{d}N \]](/images/math/9/7/7/97747d11b52f7e43952a876c7f1da697.png)
összefüggéssel egészíthetjük ki, a megoldás alakjának értelmezésében pedig az említett feladatban nyert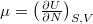 
és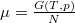 
észrevétel segít.
