„Elektrosztatika - Elektromos potenciál” változatai közötti eltérés
A Fizipedia wikiből
| 14. sor: | 14. sor: | ||
{{:Elektrosztatika példák - Összeolvadt esőcseppek potenciálja}}{{Megoldás|link=Elektrosztatika példák - Összeolvadt esőcseppek potenciálja}} | {{:Elektrosztatika példák - Összeolvadt esőcseppek potenciálja}}{{Megoldás|link=Elektrosztatika példák - Összeolvadt esőcseppek potenciálja}} | ||
{{:Elektrosztatika példák - Egyenletesen töltött fémgömb árnyékolással potenciáltere}}{{Megoldás|link=Elektrosztatika példák - Egyenletesen töltött fémgömb árnyékolással potenciáltere}} | {{:Elektrosztatika példák - Egyenletesen töltött fémgömb árnyékolással potenciáltere}}{{Megoldás|link=Elektrosztatika példák - Egyenletesen töltött fémgömb árnyékolással potenciáltere}} | ||
| − | |||
{{:Elektrosztatika példák - Koaxilális hengerfelületek potenciáltere}}{{Megoldás|link=Elektrosztatika példák - Koaxilális hengerfelületek potenciáltere}} | {{:Elektrosztatika példák - Koaxilális hengerfelületek potenciáltere}}{{Megoldás|link=Elektrosztatika példák - Koaxilális hengerfelületek potenciáltere}} | ||
{{:Elektrosztatika példák - Árnyékolt, egyenletesen töltött hengertérfogat potenciáltere}}{{Megoldás|link=Elektrosztatika példák - Árnyékolt, egyenletesen töltött hengertérfogat potenciáltere}} | {{:Elektrosztatika példák - Árnyékolt, egyenletesen töltött hengertérfogat potenciáltere}}{{Megoldás|link=Elektrosztatika példák - Árnyékolt, egyenletesen töltött hengertérfogat potenciáltere}} | ||
{{:Elektrosztatika példák - Összeolvadt felhő-vízcseppek potenciálja}}{{Megoldás|link=Elektrosztatika példák - Összeolvadt felhő-vízcseppek potenciálja}} | {{:Elektrosztatika példák - Összeolvadt felhő-vízcseppek potenciálja}}{{Megoldás|link=Elektrosztatika példák - Összeolvadt felhő-vízcseppek potenciálja}} | ||
{{:Elektrosztatika példák - Vezető félgömb potenciálja a középpontban}}{{Megoldás|link=Elektrosztatika példák - Vezető félgömb potenciálja a középpontba}} | {{:Elektrosztatika példák - Vezető félgömb potenciálja a középpontban}}{{Megoldás|link=Elektrosztatika példák - Vezető félgömb potenciálja a középpontba}} | ||
A lap 2013. június 26., 17:07-kori változata
Feladatok
- Határozzuk meg az
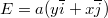 elektromos erőtér potenciálját, ha
elektromos erőtér potenciálját, ha 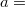 állandó,
állandó, 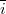 és
és 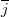 az
az  és
és  tengely irányába mutató egységvektorok!
tengely irányába mutató egységvektorok!
- Határozzuk meg az elektromos térerősség vektorát, ha a potenciál:
a)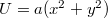
b)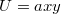
módon függ a koordinátáktól, ahol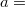 állandó!
állandó!
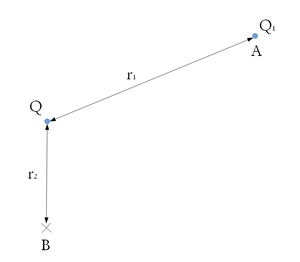
- Mekkora munkát kell végeznünk, ha a
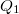 töltést az ábrán látható
töltést az ábrán látható  töltés környezetében az
töltés környezetében az  pontból a
pontból a  pontba visszük át?
pontba visszük át?
 sugarú szigetelő körlemezre
sugarú szigetelő körlemezre  töltést viszünk egyenletes felületi töltéssűrűséggel. A kör középpontja felett, a kör síkjától
töltést viszünk egyenletes felületi töltéssűrűséggel. A kör középpontja felett, a kör síkjától  távolságra mekkora a potenciál?
távolságra mekkora a potenciál?
- Két párhuzamos, nagy kiterjedésű vezető sík egyike földelt, a másik felületi töltéssűrűsége
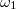 . A lemezek távolsága
. A lemezek távolsága  .
.
a) Mekkora a lemezek közötti potenciálkülönbség?
b) Mekkora lesz a potenciálkülönbség, ha a lemezekkel párhuzamosan, tőlük egyenlő távolságra, egy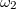 felületi töltéssűrűségű harmadik lemezt helyezünk?
felületi töltéssűrűségű harmadik lemezt helyezünk?
- Nyolc esőcsepp mindengyikének potenciálja
 . Egyetlen cseppé egyesülésük után mekkora lesz ennek a cseppnek a potenciálja?
. Egyetlen cseppé egyesülésük után mekkora lesz ennek a cseppnek a potenciálja?
- Egy
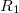 sugarú tömör fémgömböt koncentrikusan vesz körül, egy
sugarú tömör fémgömböt koncentrikusan vesz körül, egy  falvastagságú fém gömbhéj, aminek a belső átmérője
falvastagságú fém gömbhéj, aminek a belső átmérője 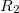 . Közöttük levegő van. A belső fémgömböt feltöltjük, úgy, hogy a felületi töltéssűrűsége
. Közöttük levegő van. A belső fémgömböt feltöltjük, úgy, hogy a felületi töltéssűrűsége  .
.
a) Határozzuk meg a számszerűen a térerősséget a gömbök felszínén.
b) Ábrázoljuk a térerősséget, mint a középponttól mért távolság függvényét, ha a külső gömb földeletlen, illetve földelt.
c) Mekkora a gömbök közötti potenciálkülönbség?
d) Legfeljebb mekkora feszültség kapcsolható a gömbökre, ha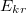 dielektromos szilárdságú szigetelőt teszünk közéjük?
dielektromos szilárdságú szigetelőt teszünk közéjük?
- Két végtelen hosszú koaxiális fémhengert egynemű töltéssel töltünk fel úgy, hogy a töltéssűrűség a külső hengeren
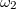 , a belsőn pedig
, a belsőn pedig 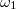 . A hengerek sugara
. A hengerek sugara 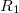 és
és 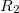 . Határozzuk meg a hengerek közötti potenciálkülönbséget?
. Határozzuk meg a hengerek közötti potenciálkülönbséget?
- Egy
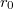 sugarú, hosszú egyenes vezető szálra ismeretlen nagyságú töltést viszünk, majd
sugarú, hosszú egyenes vezető szálra ismeretlen nagyságú töltést viszünk, majd  sugarú, vékony falú fémhengerrel vesszük körül koaxiálisan. A vezető szálon a felületi töltéssűrűség állandó. A henger töltetlen és a talajtól szigetelt, míg a szál
sugarú, vékony falú fémhengerrel vesszük körül koaxiálisan. A vezető szálon a felületi töltéssűrűség állandó. A henger töltetlen és a talajtól szigetelt, míg a szál 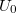 potenciálon van a tengelyétől 1 m távoli ponthoz képest.
potenciálon van a tengelyétől 1 m távoli ponthoz képest.
a) Milyen potenciálon lesz a henger?
b) Mekkora lesz a térerősség a henger külső felületén?
c) Elektromos mérésekkel kimutatható-e az -nél nagyobb távolságban a henger jelenléte a szál körül?
-nél nagyobb távolságban a henger jelenléte a szál körül?
- A felhőkben levő vízcseppeket kis sugarú gömböknek lehet tekinteni, amelyek egymástól olyan távolságban vannak, hogy töltésük a többiektől függetlenül jön létre. Tegyük fel azt, hogy a felhőt alkotó apró vízcseppek átmérője
 és átlagosan
és átlagosan  potenciálra töltődnek fel. Ha ezek az apró cseppek
potenciálra töltődnek fel. Ha ezek az apró cseppek  sugarú cseppekké sűrűsödnek, mekkora lesz a nagy cseppek potenciálja a végtelen távoli ponthoz képest?
sugarú cseppekké sűrűsödnek, mekkora lesz a nagy cseppek potenciálja a végtelen távoli ponthoz képest?
- Egy
 sugarú félgömbhéjat feltöltünk
sugarú félgömbhéjat feltöltünk  töltéssel. Mekkora a potenciál a gömb középpontjában, a végtelen távol lévő ponthoz képest? A megoldáshoz használjuk a szuperpozíció elvét.
töltéssel. Mekkora a potenciál a gömb középpontjában, a végtelen távol lévő ponthoz képest? A megoldáshoz használjuk a szuperpozíció elvét.
![\[U=-axy+C\]](/images/math/1/7/c/17cbed1f73791320a1d8440c5144e446.png)
![\[\overline{E}=-2ax\overline{i}+2ay\overline{j}\]](/images/math/2/3/b/23b229f6c30463bbb94c8c9a8e59895d.png)
![\[\overline{E}=-ay\overline{i}-ax\overline{j}\]](/images/math/9/f/5/9f5ea896b3cf8e3a9e0e8db60f8812ec.png)
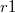 sugarú,
sugarú, ![\[W=-\dfrac{Q_1}{4\pi\varepsilon_0}\int_{r1}^{r2}\dfrac{1}{r^2}dr=-\dfrac{Q_1}{4\pi\varepsilon_0}\left( \dfrac{1}{r1}-\dfrac{1}{r2} \right)\]](/images/math/8/3/6/8364d4d6f8d43af95efb89114bcf36d8.png)
 polárkoordináták szerint, a szuperpozíció elve alapján skalárisan összegeznünk kell az egyes felületelemek
polárkoordináták szerint, a szuperpozíció elve alapján skalárisan összegeznünk kell az egyes felületelemek 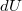 potenciál járulékait.
potenciál járulékait. ![\[U=\dfrac{Q}{2\pi\varepsilon_0 R^2}\left( \sqrt{R^2+z^2}-z\right)\]](/images/math/4/d/c/4dc49776c2a3ca89afc6003435cb5112.png)
![\[ U =\frac{\omega_{1}}{\epsilon_{0}}\cdot d \]](/images/math/c/7/9/c7966653df23b09877d552d1a8120db2.png)
![\[U = U_{1}+U_{2} = \frac{\omega_{1}+\omega_{2}}{2\cdot\epsilon_{0}}\cdot d + \frac{\omega_{1}}{\epsilon_{0}}\cdot d = \frac{2\cdot\omega_{1}+\omega_{2}}{\epsilon_{0}}\cdot \frac{d}{2} \]](/images/math/6/b/0/6b05539342a4baf3ef56a0b244911a06.png)
![\[\frac{k\cdot 8\cdot Q}{2\cdot r} = 4\cdot\frac{k\cdot Q}{r} = 4\cdot U\]](/images/math/c/6/3/c63ece0baa548b55184d358a6bf3514a.png)
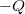 , külső felületén pedig
, külső felületén pedig ![\[\vec{E}=\frac{\omega}{\epsilon_{0}}\]](/images/math/1/5/d/15d20a6021d6601490871e3c4ed48bf7.png)
![\[\vec{E}=\frac{\omega\cdot R_{1}^{2}}{\epsilon_{0}\cdot R_{3}^{2}}\]](/images/math/6/4/b/64b193f7e3326be3691062cb198b5bc7.png)
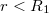
![\[\vec{E}\cdot 4\cdot r^{2}\cdot\pi = 0 \Rightarrow \vec{E}=0\]](/images/math/7/a/f/7af4f60c44b4e29f0970f81e09988426.png)
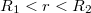
![\[\vec{E}\cdot 4\cdot r^{2}\cdot\pi = \frac{\omega}{\epsilon_{0}}\cdot 4\cdot R_{1}^{2}\cdot\pi \Rightarrow \vec{E}= \frac{\omega\cdot R_{1}^{2}}{\epsilon_{0}\cdot r^{2}}\]](/images/math/6/b/e/6be977370516a5e807b6e7cb59f99c8e.png)
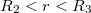
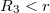
![\[ \Delta U = \frac{\omega\cdot R_{1}^{2}}{\epsilon_{0}}\cdot [\frac{1}{R_{1}}-\frac{1}{R_{2}}]\]](/images/math/f/4/c/f4c60dff9fba2256f157bc2e3afc28c9.png)
![\[ \Delta U = E_{kr}\cdot R_{1}^{2}\cdot [\frac{1}{R_{1}}-\frac{1}{R_{2}}]\]](/images/math/5/b/b/5bb8c30ad6998b0a96dd0fe6437d329e.png)
![\[\Delta U = \int_{R_{1}}^{R_{2}}\frac{\omega_{2}\cdot R_{1}}{\epsilon_{0}\cdot r}\cdot dr =\frac{\omega_{2}\cdot R_{1}}{\epsilon_{0}}\cdot \ln\left(\frac{R_{2}}{R_{1}}\right) \]](/images/math/a/3/2/a32796d7e4e70e997416c251e424b512.png)
![\[ U = -\frac{\omega}{\epsilon_{0}}\cdot r_{0}\ln\left(R\right)\]](/images/math/2/e/2/2e2bbc9e61b03b7f52995e2b36633346.png)
![\[\vec{E} = \frac{\omega\cdot r_{0}}{\epsilon_{0}\cdot R}\]](/images/math/4/4/8/4486bd1f5f3531c43c0f3997d79e4ab7.png)
![\[E=\dfrac{\omega}{2\varepsilon_{0}} \left(1-\dfrac{z}{(R^2+z^2)^{1/2}} \right)\]](/images/math/e/7/6/e760b68831c68f2b1ca6a11b95ddee89.png)
![\[U_{felgomb} = \frac{U_{gomb}}{2} = \frac{Q}{8\cdot\pi\cdot\epsilon_{0}\cdot R}\]](/images/math/7/2/f/72f1e85ee866b0a5c16a9fe027af916d.png)