Kvantummechanikai bevezető példák - Compton-szórás szabad elektronra

Feladat

1. Vizsgáljuk meg, hogy létezik-e olyan effektus, hogy egy szabad elektron teljes egészében elnyel egy fotont (teljesen rugalmatlan ütközés)! Ennek fényében, hogyan magyarázható a fotoeffektus?

Megoldás

A Compton-szórásról szóló feladatban levezettük, hogy a foton által átadott energiahányad

$\[ \eta = \frac{|\Delta E_f|}{E_f} = \frac{p_f c - p'_f c }{p_f c} = 1 - \left(\frac{p_f(1-\cos\vartheta)}{m_e c}+1\right)^{-1}. \]$

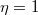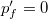Abból a feltételből, hogy az elektron a foton minden energiáját elnyeli ($\setbox0\hbox{$\eta=1$}% \message{//depth:\the\dp0//}% \box0%$ vagy $\setbox0\hbox{$p'_f=0$}% \message{//depth:\the\dp0//}% \box0%$) következik, a szórási szögre, hogy 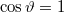$\setbox0\hbox{$\cos \vartheta = 1$}% \message{//depth:\the\dp0//}% \box0%$, azaz 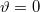$\setbox0\hbox{$\vartheta=0$}% \message{//depth:\the\dp0//}% \box0%$. Ebből vagy az energia- és impulzusmegmaradásra felírt egyenletekből látszik, hogy 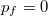$\setbox0\hbox{$p_f=0$}% \message{//depth:\the\dp0//}% \box0%$-nak is teljesülnie kellene, azaz teljes energiaelnyelés csak akkor jöhet létre, ha a kezdeti foton energiája nulla, azaz nem volt elnyelt foton, nem történt szórás. Tehát szabad elektron nem nyelhet el teljes egészében egy fotont.

A fotoeffektusnál a fotont nem szabad elektron nyeli el, az energiamegmaradást ki kell egészíteni a kilépési munkával:

$\[ p_f c + m_e c^2 = p'_f c + \sqrt{\left(m_e c^2\right)^2+\left(p'_e c\right)^2} + \Phi_0, \]$

ahol $\setbox0\hbox{$p'_f=0$}% \message{//depth:\the\dp0//}% \box0%$:

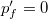$\[ \left(p_f c + m_e c^2 - \Phi_0 \right)^2 = \left(m_e c^2\right)^2+\left(p'_e c\right)^2. \]$

Az impulzusmegmaradásból most

$\[ p'_e = p_f, \]$

amivel

$\[ 2(p_f c)(m_e c^2) + \Phi_0^2 - 2 \Phi_0 (m_e c^2 + p_f c) = 0, \]$

$\[ p_f = \frac{\Phi_0^2 - 2 \Phi_0 m_e c^2}{2\Phi_0 c - 2 m_e c^3} \]$

diszkrét impulzus adódik, azaz csak 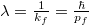$\setbox0\hbox{$\lambda=\frac{1}{k_f}=\frac{\hbar}{p_f}$}% \message{//depth:\the\dp0//}% \box0%$ hullámhosszú foton volna képes fotoeffektust kiváltani.

A fotoeffektus létrejöttét különböző (kellően nagy) frekvenciákra azzal magyarázhatjuk, hogy 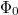$\setbox0\hbox{$\Phi_0$}% \message{//depth:\the\dp0//}% \box0%$ a szükséges minimális kilépési munka, de a fémben levő elektronok mozognak, kinetikus energiájuk tágítja a spektrumot, továbbá a fém képes a felesleges energiát termikus gerjesztéssé disszipálni.