Kvantummechanikai bevezető példák - Schrödinger-egyenlet megoldása hidrogénatomban
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kvantummechanikai bevezető |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Határozza meg a Schrödinger-féle hidrogénatomban az elektron alapállapoti hullámfüggvényét! Számítsa ki, hogy protontól milyen távolságban található meg az elektron a legnagyobb valószínűséggel!
Megoldás
A hidrogénatom Schrödinger-egyenlete
![\[ -\frac{\hbar^2}{2m}\triangle\Psi + V(r)\Psi = E\Psi, \]](/images/math/5/6/3/5631fd2ca402df7aca11a96626165bbe.png)
aminek megoldását 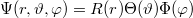 alakban érdemes keresni. A megoldás abszolútértéknégyzete (
alakban érdemes keresni. A megoldás abszolútértéknégyzete (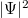 ) az elektron megtalálási valószínűsége egy adott térfogatelemben. A Schrödinger-egyenlet megoldása a szögfüggő tényezők levezetésével megtalálható a kibővített óravázlat 34-38. oldalán.
) az elektron megtalálási valószínűsége egy adott térfogatelemben. A Schrödinger-egyenlet megoldása a szögfüggő tényezők levezetésével megtalálható a kibővített óravázlat 34-38. oldalán.
A sugárirányú differenciálegyenletet 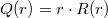 helyettesítéssel megoldva a sugárirányú eloszlás
helyettesítéssel megoldva a sugárirányú eloszlás
![\[ R(r) = A_n \left(\frac{r}{a_0}\right)^{n-1} e^{\textstyle -\frac{r}{n a_0}}, \]](/images/math/9/f/d/9fd3c90ed55f2d0d8ff424777b53c98c.png)
ahol 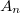 egy, a pályára jellemző normáló tényező, hogy a megtalálási valószínűség teljes térre vett integrálja
egy, a pályára jellemző normáló tényező, hogy a megtalálási valószínűség teljes térre vett integrálja  legyen.
A másik két eloszlás értéke a feladat megoldásában nem játszik szerepet, mert a szögek szerint kiintegrálva ugyanazt a sugártól független állandót adják.
legyen.
A másik két eloszlás értéke a feladat megoldásában nem játszik szerepet, mert a szögek szerint kiintegrálva ugyanazt a sugártól független állandót adják.
Az elektron megtalálási valószínűsége ![\setbox0\hbox{$[r,r+\mathrm{d}r]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/b/c/c/bcc8b3a1eda12dfc7239df89d3dee2f8.png) intervallumban tehát
intervallumban tehát
![\[ \int_0^{2\pi} \int_0^\pi |\Psi(r,\vartheta,\varphi)|^2 r^2 \sin \vartheta \,\mathrm{d}r \,\mathrm{d}\vartheta \,\mathrm{d}\varphi \sim \left[r\cdot R(r)\right]^2 \,\mathrm{d}r \]](/images/math/f/6/1/f61673d3b697a2fc76681bbd25e81fee.png)
A legvalószínűbb sugarat 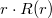 szélsőértékhelye adja:
szélsőértékhelye adja:
![\[ 0 = \left. \frac{\mathrm{d}}{\mathrm{d}r} \Big(r\cdot R(r)\Big) \right|_{r_\text{lv.}} = A_n \left[ n\left(\frac{r_\text{lv.}}{a_0}\right)^{n-1} - \frac{1}{n}\left(\frac{r_\text{lv.}}{a_0}\right)^n \right] e^{\textstyle -\frac{r_\text{lv.}}{n a_0}}, \]](/images/math/0/5/3/053824569620cab57d128596b2a222d0.png)
ami alapján 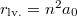 . Az alapállapotú hidrogénatomban a legvalószínűbb sugár éppen a Bohr-sugár.
. Az alapállapotú hidrogénatomban a legvalószínűbb sugár éppen a Bohr-sugár.