Kvantummechanikai bevezető példák - Relativisztikus tömegnövekedés Bohr-féle hidrogénmodellben
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kvantummechanikai bevezető |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Számítsa ki, hogy a hidrogénatom Bohr-féle modelljében a relativisztikus tömegnövekedés milyen korrekciót jelentene az energiaszintekben!
Megoldás
A Bohr-modellről szóló feladatban levezetett![\[ E_n = -\frac{e^4}{2\hbar^2(4\pi\varepsilon_0)^2} \cdot m \cdot \frac{1}{n^2} \]](/images/math/a/6/a/a6ae56a9669024863e8648da54cb29be.png)
energiakifejezésbe most az 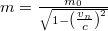 relativisztikus tömeget helyettesítjük be és sorba fejtjük a nevezőt:
relativisztikus tömeget helyettesítjük be és sorba fejtjük a nevezőt:
![\[ E_n = -\frac{E_0}{\sqrt{1-\left(\textstyle \frac{v_n}{c}\right)^2}}\cdot \frac{1}{n^2} = -E_0\left(1+\frac12\left(\frac{v_n}{c}\right)^2+O\left[\left(\frac{v_n}{c}\right)^4\right]\right)\frac{1}{n^2} \]](/images/math/b/b/1/bb197754f756cdefb45fc53562723465.png)
vagy másként a relativisztikus tömegnövekedéssel korrigált energiaszintek
![\[ E_n = -\frac{E_0}{n^2}-\frac{E_0}{2} \frac{\alpha_f^2}{n^4}+O\left[n^{-6}\right], \]](/images/math/1/9/9/199cedfdb000e94b97da397355f62e91.png)
ahol 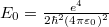 ,
, 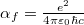 és
és 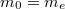 az elektron nyugalmi tömege.
az elektron nyugalmi tömege.
A mérések ezt nem támasztják alá, azaz a Bohr-modell csak egy közelítő leírása a hidrogénatomnak, mint kvantummechanikai objektumnak. A pontos eredmény a Klein–Gordon-formula:
![\[ E_n = m_0 c^2 - \frac{m_0 e^4}{2\hbar^2(4\pi\varepsilon_0)^2} \frac{1}{n^2} + \frac34 \frac{m_0 e^8}{2\hbar^4(4\pi\varepsilon_0)^2} \frac{1}{n^4} +O\left[n^{-6}\right] \]](/images/math/8/1/7/8177499678e0d0bdb30e5ed2dc4ff5bd.png)
az előző jelölésekkel
![\[ E_n = mc^2 - \frac{E_0}{n^2} - \frac{3E_0}{4} \frac{\alpha_f^2}{n^4}+O\left[n^{-6}\right], \]](/images/math/5/3/4/5343d50b97332c633abf61769b7eec46.png)
ahol az első tag az tömeg-energia megfeleltetésből adódó kifejezés, a második tag a nemrelativisztikus eredmény, a harmadik tagban, pedig már a klasszikus relativisztikus tárgyalás hibája jelenik meg.