Kvantummechanikai bevezető példák - Foton és elektron kinetikus energiája a hullámszám függvényében

Feladat

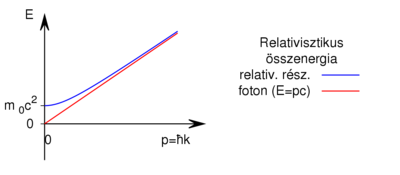
1. Hasonlítsa össze a foton és az elektron kinetikus energia-hullámszám görbéjét! Elemezze a lehetséges jellegzetességeket relativisztikus, és nemrelativisztikus esetekben!

Megoldás

A relativisztikus összenergia

$\[ E(\mathbf{p}) = \sqrt{m_0^2c^4+c^2p^2}, \]$

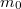ahol $\setbox0\hbox{$m_0$}% \message{//depth:\the\dp0//}% \box0%$ a részecske nyugalmi tömege, 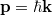$\setbox0\hbox{$\mathbf{p}=\hbar \mathbf{k}$}% \message{//depth:\the\dp0//}% \box0%$ pedig a relativisztikus impulzusa kifejezve a 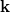$\setbox0\hbox{$\mathbf{k}$}% \message{//depth:\the\dp0//}% \box0%$ hullámszámmal. Ebből kivonva a nyugalmi energiát a kinetikus energiát kapjuk:

$\[ E_\text{kin}(\mathbf{k}) = E(\mathbf{\hbar k}) - m_0c^2. \]$

A foton nyugalmi tömege nulla, ezért az

$\[ E_\text{kin}^\text{foton}(\mathbf{k}) = \hbar |\mathbf{k}| c \]$

diszperziós relációja lineáris.

Kis sebességekre 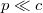$\setbox0\hbox{$p\ll c$}% \message{//depth:\the\dp0//}% \box0%$ (nemrelativisztikus tartomány) a kinetikus energia sorba fejthető

$\[ E_\text{kin}(\mathbf{k}) = m_0c^2 \left[ \sqrt{1+\left(\frac{p}{m_0 c}\right)^2} - 1 \right] = m_0c^2 \left[ 1+\frac12\left(\frac{p}{m_0 c}\right)^2 + O(p^4) - 1 \right] =\frac{p^2}{2m_0} + O(p^4), \]$

és visszakapjuk a newtoni viselkedést a négyzetes diszperziós relációval.