Kvantummechanikai bevezető példák - Nap felszíni hőmérsékletének becslése

Feladat

1. Nyári napsütésben, délben a Föld felszínének 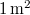$\setbox0\hbox{$1\,\mathrm{m^2}$}% \message{//depth:\the\dp0//}% \box0%$-én átlagosan kb. 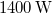$\setbox0\hbox{$1400\,\mathrm{W}$}% \message{//depth:\the\dp0//}% \box0%$ napsugárzási teljesítmény mérhető. Becsüljük meg a Nap felszínének hőmérsékletét!
   ($\setbox0\hbox{$\sigma =5{,}671\cdot {10}^{-8}\mathrm{\frac W{m^2\,K^4}}$}% \message{//depth:\the\dp0//}% \box0%$)

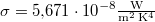Megoldás

A Stefan–Boltzmann-féle sugárzási törvény szerint, ha a Nap felszíne $\setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0%$ hőmérsékletű, a felületegységenként kisugárzott teljesítmény

$\[ \mathcal{E}_t = \sigma T^4. \]$

A Nap felszínén kisugárzott összes teljesítmény egyenletesen oszlik el a földpályát tartalmazó (közelítőleg gömb alakú) felületen:

$\[ \mathcal{E}_t 4\pi R_N^2 = \mathcal{E}_t^* 4\pi d^2, \]$

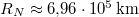ahol $\setbox0\hbox{$R_N \approx 6{,}96 \cdot 10^5\,\mathrm{km}$}% \message{//depth:\the\dp0//}% \box0%$ a Nap átlagos sugara, 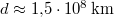$\setbox0\hbox{$d \approx 1{,}5 \cdot 10^{8}\,\mathrm{km}$}% \message{//depth:\the\dp0//}% \box0%$ a Föld átlagos távolsága a Naptól, 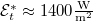$\setbox0\hbox{$\mathcal{E}_t^* \approx 1400 \mathrm{\frac{W}{m^2}}$}% \message{//depth:\the\dp0//}% \box0%$ pedig az egységnyi felületre jutó sugárzási teljesítmény a Föld távolságában.

Ezek alapján

$\[ T^4 = \frac{\mathcal{E}_t}{\sigma} = \frac{\mathcal{E}_t^*}{\sigma} \left( \frac{d}{R_N} \right)^2, \]$

az adatokat behelyettesítve

$\[ T = 5819\,\mathrm{K}, \]$

ami megfelel a szakirodalmi értéknek. (Vö. számítógépképernyők meleg színárnyalatához 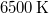$\setbox0\hbox{$6500\,\mathrm{K}$}% \message{//depth:\the\dp0//}% \box0%$ hőmérsékletet rendelnek.)

Megjegyzés

A Wien-féle eltolódási törvény szerint a hőmérséklet és a legnagyobb intenzitással sugárzott hullámhossz közt fordított arányosság áll fenn:

$\[ \lambda_\text{max} \cdot T = 2{,}898 \cdot 10^{-3} \,\mathrm{m \cdot K}, \]$

ami alapján a Nap 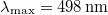$\setbox0\hbox{$ \lambda_\text{max} = 498\,\mathrm{nm} $}% \message{//depth:\the\dp0//}% \box0%$ hullámhosszon sugároz legintenzívebben. Szerencsénkre ez éppen a látható 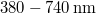$\setbox0\hbox{$380-740\,\mathrm{nm}$}% \message{//depth:\the\dp0//}% \box0%$ tartomány közepére esik, így jól láthatunk; még jobb magyarázat, miszerint az evolúció alakította úgy a látásunkat, hogy abban a tartományban lássunk, ahol legtöbb a fény. :-)