„Kvantummechanikai bevezető” változatai közötti eltérés
A Fizipedia wikiből
a |
a (Kereshetőség érdekében a hosszú kötőjeles szavakat tagolom) |
||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 10. sor: | 10. sor: | ||
== Ismert fizikai állandók == | == Ismert fizikai állandók == | ||
<wlatex>{| style="margin-left: auto; margin-right: auto;" | <wlatex>{| style="margin-left: auto; margin-right: auto;" | ||
| − | | align="right" | $k$ || = || $1{,}381 \cdot 10^{-23}\,\mathrm{J \cdot K^{-1}}$ || Boltzmann-állandó | + | | align="right" | $k$ || = || $1{,}381 \cdot 10^{-23}\,\mathrm{J \cdot K^{-1}}$ || ''Boltzmann''-állandó |
|- | |- | ||
| − | | align="right" | $h$ || = || $6{,}626 \cdot 10^{-34}\,\mathrm{J \cdot s}$ || Planck-állandó ($h=2\pi \hbar$) | + | | align="right" | $h$ || = || $6{,}626 \cdot 10^{-34}\,\mathrm{J \cdot s}$ || ''Planck''-állandó ($h=2\pi \hbar$) |
|- | |- | ||
| − | | align="right" | $\sigma$ || = || $5{,}671 \cdot 10^{-8}\,\mathrm{W \cdot m^{-2} \cdot K^{-4}}$ || Stefan | + | | align="right" | $\sigma$ || = || $5{,}671 \cdot 10^{-8}\,\mathrm{W \cdot m^{-2} \cdot K^{-4}}$ || ''Stefan''–''Boltzmann''-állandó |
|- | |- | ||
| align="right" | $c$ || = || $2{,}998 \cdot 10^{8}\,\mathrm{m \cdot s^{-1}}$ || vákuumbeli fénysebesség | | align="right" | $c$ || = || $2{,}998 \cdot 10^{8}\,\mathrm{m \cdot s^{-1}}$ || vákuumbeli fénysebesség | ||
| 24. sor: | 24. sor: | ||
| align="right" | $m_p$ || = || $1{,}672 \cdot 10^{-27}\,\mathrm{kg}$ || proton tömege ($m_p\approx 1835\,m_e$) | | align="right" | $m_p$ || = || $1{,}672 \cdot 10^{-27}\,\mathrm{kg}$ || proton tömege ($m_p\approx 1835\,m_e$) | ||
|- | |- | ||
| − | | align="right" | $R$ || = || $3{,}289 \cdot 10^{15}\,\mathrm{s^{-1}}$ || Rydberg-állandó | + | | align="right" | $R$ || = || $3{,}289 \cdot 10^{15}\,\mathrm{s^{-1}}$ || ''Rydberg''-állandó |
|- | |- | ||
| align="right" | $\alpha_f$ || = || $ 1/137{,}036 $ || finomszerkezeti állandó ($\alpha_f = \frac{e^2}{4\pi \varepsilon_0\hbar c}$) | | align="right" | $\alpha_f$ || = || $ 1/137{,}036 $ || finomszerkezeti állandó ($\alpha_f = \frac{e^2}{4\pi \varepsilon_0\hbar c}$) | ||
A lap jelenlegi, 2013. július 1., 14:35-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kvantummechanikai bevezető |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Ismert fizikai állandók
 |
= | 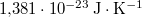 |
Boltzmann-állandó |
 |
= | 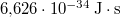 |
Planck-állandó (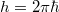 ) )
|
 |
= | 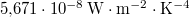 |
Stefan–Boltzmann-állandó |
 |
= | 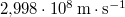 |
vákuumbeli fénysebesség |
 |
= | 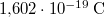 |
elemi töltés |
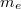 |
= | 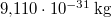 |
elektron tömege |
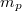 |
= | 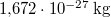 |
proton tömege (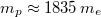 ) )
|
 |
= | 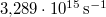 |
Rydberg-állandó |
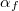 |
= | 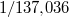 |
finomszerkezeti állandó (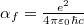 ) )
|
Feladatok
- Nyári napsütésben, délben a Föld felszínének
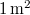 -én átlagosan kb.
-én átlagosan kb. 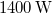 napsugárzási teljesítmény mérhető. Becsüljük meg a Nap felszínének hőmérsékletét!
napsugárzási teljesítmény mérhető. Becsüljük meg a Nap felszínének hőmérsékletét!
(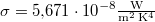 )
)
- Egy izzólámpában a volfrámszál hőmérséklete kb.
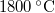 . Az emberi szem a
. Az emberi szem a 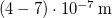 hullámhossz tartományban lát. Becsülje meg az izzólámpa „hatásfokát”!
hullámhossz tartományban lát. Becsülje meg az izzólámpa „hatásfokát”!
- Határozzuk meg, hogy egy
 hőmérséklet fekete test milyen foton-áramsűrűséggel sugároz!
hőmérséklet fekete test milyen foton-áramsűrűséggel sugároz!
- Egy
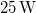 -os megfelelő gázzal töltött lámpától
-os megfelelő gázzal töltött lámpától 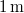 -re egy tantál fémfelületet (
-re egy tantál fémfelületet (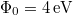 ) helyezünk el. A klasszikus elmélet alapján becsülje meg, hogy egy elektron átlagosan mennyi idő alatt gyűjtene össze annyi energiát, amivel kiléphet a fémből!
) helyezünk el. A klasszikus elmélet alapján becsülje meg, hogy egy elektron átlagosan mennyi idő alatt gyűjtene össze annyi energiát, amivel kiléphet a fémből!
(A valóságban a fotoeffektus során az elektronok a megvilágításkor „azonnal” kilépnek a fémből.)
- Határozza meg, hogy a Compton-szórás esetén a beeső foton energiájának hány százalékát adja le az elektronnak!
- Vizsgáljuk meg, hogy létezik-e olyan effektus, hogy egy szabad elektron teljes egészében elnyel egy fotont (teljesen rugalmatlan ütközés)! Ennek fényében, hogyan magyarázható a fotoeffektus?
- Alkalmazza a Bohr–Sommerfeld-féle kvantálási hipotézist körpályán mozgó elektronra és egy lineáris oszcillátorra! Magyarázza meg a szupravezetésnél fellépő „fluxuskvantálás” jelenségét a Bohr–Sommerfeld-féle kvantálási hipotézis segítségével!
- Számítsa ki a hidrogénatom Bohr-féle modelljében a „körpályán” keringő elektron pályasugarát, sebességét, perdületét és energiáját!
- Számítsa ki, hogy a hidrogénatom Bohr-féle modelljében a relativisztikus tömegnövekedés milyen korrekciót jelentene az energiaszintekben!
- Számítsa ki, hogy a hidrogénatom Bohr-féle modelljében a mag véges nagyságú tömege milyen korrekciót jelentene az energiaszintekben és a spektrumban!
- Határozza meg, hogy az atomok fotonkibocsátásakor fellépő visszalökődés milyen korrekciót jelent az emissziós spektrumban!
- Mutassa meg, hogy miként teljesül a „korrespondencia-elv” a hidrogénatom Bohr-féle modelljében a fénykibocsátása esetén!
- Hasonlítsa össze a foton és az elektron kinetikus energia-hullámszám görbéjét! Elemezze a lehetséges jellegzetességeket relativisztikus, és nemrelativisztikus esetekben!
- Határozza meg a Schrödinger-féle hidrogénatomban az elektron alapállapoti hullámfüggvényét! Számítsa ki, hogy protontól milyen távolságban található meg az elektron a legnagyobb valószínűséggel!
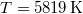
![\[\frac{\Delta \mathcal{E}}{\mathcal{E}_t}=0{,}355\%\]](/images/math/e/a/1/ea1bc4434817421fb132a20eb6e23fd8.png)
![\[N = 2{,}404 \frac{8\pi}{c^2}\left(\frac{kT}{h}\right)^3\]](/images/math/5/2/5/525d3b6c79fc0b7e9c3c5bc6bbcf4e34.png)
![\[\Delta t= \frac{16\Phi_0}{P} \left( \frac{\ell}{D_\mathrm{Ta}} \right)^2 = 4{,}88\,\mathrm{s}\]](/images/math/a/9/0/a90e4994c9b40edbfb9deab6614d74db.png)
![\[\eta = 1 - \left(\frac{p_f(1-\cos\vartheta)}{m_e c}+1\right)^{-1},\]](/images/math/e/3/d/e3d6a9c5338b3763b4cad5550a858ae6.png)
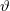 a foton eltérülése eredeti irányától.
a foton eltérülése eredeti irányától. 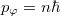 , lineáris oszcillátorra
, lineáris oszcillátorra 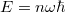 .
. ![\[ v_n = \frac{v_0}{n}, \qquad r_n = a_0 n^2,\]](/images/math/b/e/f/befdf1be2cd0570bc1714f3c8617241f.png)
![\[L_n = n\hbar, \qquad E_n = -\frac{E_0}{n^2}, \]](/images/math/f/b/6/fb6b76901bce25c085edd4b2973f8e77.png)
![\[v_0 = \frac{e^2}{4\pi\varepsilon_0\hbar}, \qquad a_0 = \frac{\hbar^2 4 \pi \varepsilon_0}{m_e e^2}, \]](/images/math/4/9/9/4999909021a110d647609282a1008127.png)
![\[ E_0 = \frac{m_e e^4}{2\hbar^2(4\pi\varepsilon_0)^2}.\]](/images/math/e/3/2/e3286e30266aeb2eb0d27f902ea46e8c.png)
![\[ E_n = -\frac{E_0}{n^2}-\frac{E_0}{2} \frac{\alpha_f^2}{n^4}+O\left[n^{-6}\right], \]](/images/math/1/9/9/199cedfdb000e94b97da397355f62e91.png)
 -ben negyedrendű korrekciót kapunk. Megjegyzendő, hogy az együttható nem pontos, mert a klasszikus relativisztikus tárgyalás nem juthat el arra a helyes eredményre, ami a kvantummechanikában a Klein–Gordon-formula néven ismert.
-ben negyedrendű korrekciót kapunk. Megjegyzendő, hogy az együttható nem pontos, mert a klasszikus relativisztikus tárgyalás nem juthat el arra a helyes eredményre, ami a kvantummechanikában a Klein–Gordon-formula néven ismert. ![\[E_n^* = -\frac{E_0}{n^2},\]](/images/math/6/e/e/6ee9b65a150eb583861a491351b3a4f1.png)
![\[ E_0^* = \frac{E_0}{1+\textstyle \frac{m_e}{M}} \approx E_0 \left(1- \frac{m_e}{M}\right), \]](/images/math/3/c/f/3cfa608d96f63f174a55fb8b88a36a1c.png)
 pedig az atommag tömege.
pedig az atommag tömege. ![\[\nu' \approx \frac{\nu}{1+\displaystyle \frac{h\nu}{Mc^2}},\]](/images/math/b/3/4/b3456225f815bfd0b26120dce20131a2.png)
 a visszalökődés nélküli foton frekvenciája,
a visszalökődés nélküli foton frekvenciája, 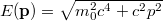 .
. ![\[ R(r) = A_n \left(\frac{r}{a_0}\right)^{n-1} e^{\textstyle -\frac{r}{n a_0}}.\]](/images/math/c/0/f/c0f960f3b75cc266fda2e137a4acc04b.png)
![\[r_\text{lv.}=n^2 a_0\]](/images/math/b/a/7/ba7a51917aa422072b054ff3f54a2da0.png)