„Kvantummechanikai bevezető példák - Tantál kilépési munkája” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Kvantummechanikai bevezető {{Kísérleti fizika gyakorlat …”) |
a (Szöveg koherenssé tétele) |
||
| (egy szerkesztő 4 közbeeső változata nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Egy $25\,\mathrm{W}$-os megfelelő gázzal töltött lámpától $1\,\mathrm{m}$-re egy | + | </noinclude><wlatex># Egy $25\,\mathrm{W}$-os megfelelő gázzal töltött lámpától $1\,\mathrm{m}$-re egy tantál fémfelületet ($\Phi_0=4\,\mathrm{eV}$) helyezünk el. A klasszikus elmélet alapján becsülje meg, hogy egy elektron átlagosan mennyi idő alatt gyűjtene össze annyi energiát, amivel kiléphet a fémből!<br />(A valóságban a fotoeffektus során az elektronok a megvilágításkor „azonnal” kilépnek a fémből.)</wlatex><includeonly><wlatex>{{Útmutatás|content=Használja fel, hogy az izzó által kibocsátott összes sugárzási teljesítmény egyenletesen oszlik el az $1\,\mathrm{m}$ sugarú gömbfelületen.}}{{Végeredmény|content=$$\Delta t= \frac{16\Phi_0}{P} \left( \frac{\ell}{D_\mathrm{Ta}} \right)^2 = 4{,}88\,\mathrm{s}$$}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>Az energiaáram-sűrűség a $P=25\,\mathrm{W}$-os izzótól $\ell=1\,\mathrm{m}$ távolságban |
| + | $$ J_e = \frac{P}{4\pi \ell^2}. $$ | ||
| + | Az egy tantálatomra jutó teljesítmény | ||
| + | $$ P_\mathrm{Ta} = J_e \frac{D_\mathrm{Ta}^2\pi}{4} = \frac{P}{16} \left( \frac{D_\mathrm{Ta}}{\ell} \right)^2, $$ | ||
| + | ahol $ D_\mathrm{Ta}\approx 290\,\mathrm{pm} $ a [http://www.webelements.com/tantalum/atom_sizes.html tantál atom átmérője]. | ||
| + | |||
| + | Az átlagos idő, ami alatt egy atom összegyűjtheti a szükséges kilépési munkát: | ||
| + | $$ \Delta t = \frac{\Phi_0}{P_\mathrm{Ta}} | ||
| + | = \frac{4 \cdot 1{,}602 \cdot 10^{-19}\,\mathrm{J}}{ 1{,}314 \cdot 10^{-19}\,\mathrm{W}} = 4{,}88\,\mathrm{s}. $$ | ||
| + | (Megjegyzendő, hogy a kilépési munkát az anyag szilárd halmazállapotában, az ionizációs energiát az anyag atomos – gáz – halmazállapotában használjuk, a kettő általában nem egyezik meg.) | ||
| + | |||
| + | A gyakorlatban már egyszerű kísérleti elrendezésekben is kimérhetjük, hogy az első kilépő elektronok $\mathrm{\mu s}$-nál kisebb időskálán megjelennek, ami alátámasztja, hogy az energiát fotonok hordozzák, és egy fotont pontosan egy atom nyelhet el. Ha a foton energiája (frekvenciája) elég nagy, akkor lesznek kilépő elektronok, különben az energia a szilárdtest termikus gerjesztésébe disszipálódik. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. június 13., 22:29-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kvantummechanikai bevezető |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy
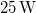-os megfelelő gázzal töltött lámpától 
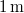-re egy tantál fémfelületet (
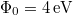) helyezünk el. A klasszikus elmélet alapján becsülje meg, hogy egy elektron átlagosan mennyi idő alatt gyűjtene össze annyi energiát, amivel kiléphet a fémből!
(A valóságban a fotoeffektus során az elektronok a megvilágításkor „azonnal” kilépnek a fémből.)
Megoldás
Az energiaáram-sűrűség a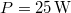 
-os izzótól 
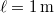távolságban
![\[ J_e = \frac{P}{4\pi \ell^2}. \]](/images/math/c/c/a/cca04c2e7440c467249836e20d54d63f.png)
Az egy tantálatomra jutó teljesítmény
![\[ P_\mathrm{Ta} = J_e \frac{D_\mathrm{Ta}^2\pi}{4} = \frac{P}{16} \left( \frac{D_\mathrm{Ta}}{\ell} \right)^2, \]](/images/math/5/5/a/55af8443ef4ba0a71b6acca292d4e525.png)
ahol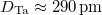 
a tantál atom átmérője.
Az átlagos idő, ami alatt egy atom összegyűjtheti a szükséges kilépési munkát:
![\[ \Delta t = \frac{\Phi_0}{P_\mathrm{Ta}} = \frac{4 \cdot 1{,}602 \cdot 10^{-19}\,\mathrm{J}}{ 1{,}314 \cdot 10^{-19}\,\mathrm{W}} = 4{,}88\,\mathrm{s}. \]](/images/math/2/9/c/29cdfa525dc7df9b7c376b8f4766bc54.png)
(Megjegyzendő, hogy a kilépési munkát az anyag szilárd halmazállapotában, az ionizációs energiát az anyag atomos – gáz – halmazállapotában használjuk, a kettő általában nem egyezik meg.)
A gyakorlatban már egyszerű kísérleti elrendezésekben is kimérhetjük, hogy az első kilépő elektronok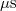 
-nál kisebb időskálán megjelennek, ami alátámasztja, hogy az energiát fotonok hordozzák, és egy fotont pontosan egy atom nyelhet el. Ha a foton energiája (frekvenciája) elég nagy, akkor lesznek kilépő elektronok, különben az energia a szilárdtest termikus gerjesztésébe disszipálódik.
