„Kvantummechanikai bevezető példák - Compton-szórás energiaviszonyai” változatai közötti eltérés
A Fizipedia wikiből
a (Kereshetőség érdekében a hosszú kötőjeles szavakat tagolom) |
|||
| (egy szerkesztő 3 közbeeső változata nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Határozza meg, hogy a Compton-szórás esetén a beeső foton energiájának hány százalékát adja le az elektronnak!</wlatex><includeonly><wlatex>{{Útmutatás|content=A Compton-szórás levezetéséhez írja fel a relativisztikus energia- és impulzusmegmaradást.}}{{Végeredmény|content=$$\eta = 1 - \left(\frac{p_f(1-\cos\vartheta)}{m_e c}+1\right)^{-1},$$ ahol $\vartheta$ a foton eltérülése eredeti irányától.}}</wlatex></includeonly><noinclude> | + | </noinclude><wlatex># Határozza meg, hogy a ''Compton''-szórás esetén a beeső foton energiájának hány százalékát adja le az elektronnak!</wlatex><includeonly><wlatex>{{Útmutatás|content=A ''Compton''-szórás levezetéséhez írja fel a relativisztikus energia- és impulzusmegmaradást.}}{{Végeredmény|content=$$\eta = 1 - \left(\frac{p_f(1-\cos\vartheta)}{m_e c}+1\right)^{-1},$$ ahol $\vartheta$ a foton eltérülése eredeti irányától.}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A Compton-szórás a fotonok elektronokon való szóródásának relativisztikus elmélete. Egy részecske relativisztikus energiája | + | <wlatex>A ''Compton''-szórás a fotonok elektronokon való szóródásának relativisztikus elmélete. Egy részecske relativisztikus energiája |
$$ E = \left(mc^2\right)^2+\left(pc\right)^2, $$ | $$ E = \left(mc^2\right)^2+\left(pc\right)^2, $$ | ||
| − | ahol $m$ a részecske nyugalmi tömege, $p=\frac{\left(mv\right)^2}{1-\textstyle \left(\frac{v}{c}\right)^2}$ relativisztikus impulzusa. | + | ahol $m$ a részecske nyugalmi tömege, $p=\frac{\left(mv\right)^2}{1-\textstyle \left(\frac{v}{c}\right)^2}$ a relativisztikus impulzusa. |
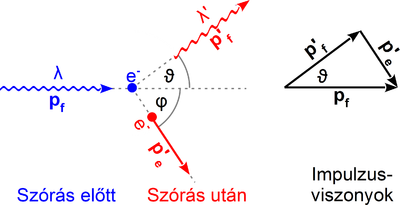
Vizsgáljuk azt az esetet, amikor a $p_f$ kezdeti impulzusú foton egy nyugalomban lévő ($p_e=0$) elektronon szóródik (ezt a koordinátarendszer megfelelő választásával könnyen elérhetjük). Az energiamegmaradás szerint | Vizsgáljuk azt az esetet, amikor a $p_f$ kezdeti impulzusú foton egy nyugalomban lévő ($p_e=0$) elektronon szóródik (ezt a koordinátarendszer megfelelő választásával könnyen elérhetjük). Az energiamegmaradás szerint | ||
| 19. sor: | 20. sor: | ||
$$ \left(p_f c - p'_f c + m_e c^2\right)^2 = \left(m_e c^2\right)^2+\left(p'_e c\right)^2. $$ | $$ \left(p_f c - p'_f c + m_e c^2\right)^2 = \left(m_e c^2\right)^2+\left(p'_e c\right)^2. $$ | ||
| − | Az impulzusmegmaradás szerint | + | |
| + | [[Fájl:Compton-szórás.png|center|400px]] | ||
| + | |||
| + | |||
| + | Az impulzusmegmaradás szerint | ||
$$ {p'_e}^2 = p_f^2 + {p'_f}^2 - 2 p_f p'_f \cos \vartheta, $$ | $$ {p'_e}^2 = p_f^2 + {p'_f}^2 - 2 p_f p'_f \cos \vartheta, $$ | ||
| − | ahol $\vartheta$ a foton eredeti irányától való | + | ahol $\vartheta$ a foton eredeti irányától való eltérésének szöge. Ezzel az előző egyenlet |
$$ -2(1-\cos \vartheta)p_f p'_f c^2 + 2(p_f c)(m_e c^2) -2(p'_f c)(m_e c^2) = 0 $$ | $$ -2(1-\cos \vartheta)p_f p'_f c^2 + 2(p_f c)(m_e c^2) -2(p'_f c)(m_e c^2) = 0 $$ | ||
| − | alakot ölti | + | alakot ölti, továbbá |
$$ 1-\cos \vartheta = \frac{m_e c}{p'_f} - \frac{m_e c}{p_f} = \frac{m_e c}{h} (\lambda'-\lambda). $$ | $$ 1-\cos \vartheta = \frac{m_e c}{p'_f} - \frac{m_e c}{p_f} = \frac{m_e c}{h} (\lambda'-\lambda). $$ | ||
| 29. sor: | 34. sor: | ||
$$ \eta = \frac{|\Delta E_f|}{E_f} = \frac{p_f c - p'_f c }{p_f c} | $$ \eta = \frac{|\Delta E_f|}{E_f} = \frac{p_f c - p'_f c }{p_f c} | ||
= 1 - \left(\frac{p_f(1-\cos\vartheta)}{m_e c}+1\right)^{-1}. $$ | = 1 - \left(\frac{p_f(1-\cos\vartheta)}{m_e c}+1\right)^{-1}. $$ | ||
| − | Az $(1-\eta)$ kifejezés | + | Az $(1-\eta)$ kifejezés megjelenik a fotonszórás differenciális hatáskeresztmetszetét megadó ''Klein''–''Nishina''-formulában is. |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. július 1., 13:37-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kvantummechanikai bevezető |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Határozza meg, hogy a Compton-szórás esetén a beeső foton energiájának hány százalékát adja le az elektronnak!
Megoldás
A Compton-szórás a fotonok elektronokon való szóródásának relativisztikus elmélete. Egy részecske relativisztikus energiája
![\[ E = \left(mc^2\right)^2+\left(pc\right)^2, \]](/images/math/a/7/6/a766f707b18184a9822b23de3c05496b.png)
ahol  a részecske nyugalmi tömege,
a részecske nyugalmi tömege, 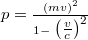 a relativisztikus impulzusa.
a relativisztikus impulzusa.
Vizsgáljuk azt az esetet, amikor a 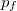 kezdeti impulzusú foton egy nyugalomban lévő (
kezdeti impulzusú foton egy nyugalomban lévő (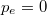 ) elektronon szóródik (ezt a koordinátarendszer megfelelő választásával könnyen elérhetjük). Az energiamegmaradás szerint
) elektronon szóródik (ezt a koordinátarendszer megfelelő választásával könnyen elérhetjük). Az energiamegmaradás szerint
![\[ p_f c + m_e c^2 = p'_f c + \sqrt{\left(m_e c^2\right)^2+\left(p'_e c\right)^2}, \]](/images/math/7/6/c/76c688421c6a1d0285458b069e604d47.png)
![\[ \left(p_f c - p'_f c + m_e c^2\right)^2 = \left(m_e c^2\right)^2+\left(p'_e c\right)^2. \]](/images/math/4/8/c/48c701f1cc640de348231691b86b52dd.png)
Az impulzusmegmaradás szerint
![\[ {p'_e}^2 = p_f^2 + {p'_f}^2 - 2 p_f p'_f \cos \vartheta, \]](/images/math/6/1/b/61bcfb29abbf63d3f91537c6d8b0d994.png)
ahol 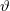 a foton eredeti irányától való eltérésének szöge. Ezzel az előző egyenlet
a foton eredeti irányától való eltérésének szöge. Ezzel az előző egyenlet
![\[ -2(1-\cos \vartheta)p_f p'_f c^2 + 2(p_f c)(m_e c^2) -2(p'_f c)(m_e c^2) = 0 \]](/images/math/c/e/1/ce16020e71134de60ffce342d670aec1.png)
alakot ölti, továbbá
![\[ 1-\cos \vartheta = \frac{m_e c}{p'_f} - \frac{m_e c}{p_f} = \frac{m_e c}{h} (\lambda'-\lambda). \]](/images/math/0/1/4/014e06d868ebcc58d9d7afa8ac51e075.png)
A foton által átadott energiahányad
![\[ \eta = \frac{|\Delta E_f|}{E_f} = \frac{p_f c - p'_f c }{p_f c} = 1 - \left(\frac{p_f(1-\cos\vartheta)}{m_e c}+1\right)^{-1}. \]](/images/math/6/e/8/6e84c0ee9d137542c0c4866ac196798c.png)
Az 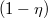 kifejezés megjelenik a fotonszórás differenciális hatáskeresztmetszetét megadó Klein–Nishina-formulában is.
kifejezés megjelenik a fotonszórás differenciális hatáskeresztmetszetét megadó Klein–Nishina-formulában is.