„Kvantummechanikai bevezető példák - Bohr-féle hidrogénmodell” változatai közötti eltérés

A Fizipedia wikiből
9. sor: 9. sor:
 
}}
 
}}
 
== Feladat ==
 
== Feladat ==
−
</noinclude><wlatex># Számítsa ki a hidrogénatom Bohr-féle modelljében a „körpályán” keringő elektron pályasugarát, sebességét, perdületét és energiáját!</wlatex><includeonly><wlatex>{{Útmutatás|content=$$keplet$$}}{{Végeredmény|content=$$keplet$$}}</wlatex></includeonly><noinclude>
+
</noinclude><wlatex># Számítsa ki a hidrogénatom Bohr-féle modelljében a „körpályán” keringő elektron pályasugarát, sebességét, perdületét és energiáját!</wlatex><includeonly><wlatex>{{Útmutatás|content=Írja fel a körpályán tartó Coulomb-erőt és alkalmazza a kvantumhipotézist!}}{{Végeredmény|content=$$ v_n = \frac{v_0}{n}, \qquad r_n = a_0 n^2,$$ $$L_n = n\hbar, \qquad E_n = -\frac{E_0}{n^2}, $$ ahol $$v_0 = \frac{e^2}{4\pi\varepsilon_0\hbar}, \qquad a_0 = \frac{\hbar^2 4 \pi \varepsilon_0}{m_e e^2}, $$ $$ E_0 = \frac{m_e e^4}{2\hbar^2(4\pi\varepsilon_0)^2}.$$}}</wlatex></includeonly><noinclude>
 
== Megoldás ==
 
== Megoldás ==
 
<wlatex>A Bohr-féle hidrogénmodellben az elektron a rögzített atommag körül kering, impulzusmomentum a [[Kvantummechanikai bevezető példák - Fluxuskvantálás szemléletesen|3. posztulátum szerint kvantált]], az $n$. pályán:
 
<wlatex>A Bohr-féle hidrogénmodellben az elektron a rögzített atommag körül kering, impulzusmomentum a [[Kvantummechanikai bevezető példák - Fluxuskvantálás szemléletesen|3. posztulátum szerint kvantált]], az $n$. pályán:
−
$$ L_n \equiv m_0 v_n r_n = n\hbar. $$
+
$$ L_n \equiv m_e v_n r_n = n\hbar. $$
−
A pályasugarakat és sebességeket a klasszikus képben végzet számításokból kapjuk: az atommag $F_C=\frac{1}{4\pi\varepsilon_0}{e^2}{r^2}$ Coulomb-vonzása az $F_{cp}=m_0 a_{cp}$ centripetális erő, ami körpályán tartja az elektront:
+
A pályasugarakat és sebességeket a klasszikus képben végzet számításokból kapjuk: az atommag $F_C=\frac{1}{4\pi\varepsilon_0}{e^2}{r^2}$ Coulomb-vonzása az $F_{cp}=m_e a_{cp}$ centripetális erő, ami körpályán tartja az elektront:
−
$$ \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r^2} = m_0 \frac{v^2}{r}. $$
+
$$ \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r^2} = m_e \frac{v^2}{r}. $$
−
$r$-rel való egyszerűsítés után beírjuk a kvantumgfeltételből kapott $r_n = \frac{n\hbar}{m_0 v_n}$ összefüggést, akkor a sebesség, és így a sugár lehetséges értékei rendre
+
$r$-rel való egyszerűsítés után beírjuk a kvantumgfeltételből kapott $r_n = \frac{n\hbar}{m_e v_n}$ összefüggést, akkor a sebesség, és így a sugár lehetséges értékei rendre
−
$$ v_n = \frac{v_0}{n} = \alpha_f \frac{c}{n}, \qquad r_n = a_0 n^2 = \frac{n^2\hbar}{\alpha_f m_0 c}, $$
+
$$ v_n = \frac{v_0}{n} = \alpha_f \frac{c}{n}, \qquad r_n = a_0 n^2 = \frac{n^2\hbar}{\alpha_f m_e c}, $$
 
ahol a legnagyobb pályasebesség és a Bohr-sugár rendre
 
ahol a legnagyobb pályasebesség és a Bohr-sugár rendre
−
$$ v_0 = \frac{e^2}{4\pi\varepsilon_0\hbar}, \qquad a_0 = \frac{\hbar^2 4 \pi \varepsilon_0}{m_0 e^2} $$
+
$$ v_0 = \frac{e^2}{4\pi\varepsilon_0\hbar}, \qquad a_0 = \frac{\hbar^2 4 \pi \varepsilon_0}{m_e e^2} $$
 
$$ v_0 \approx 2{,}187 \cdot 10^6\,\mathrm{\frac{m}{s}}, \qquad a_0 \approx 5{,}292 \cdot 10^{-11}\,\mathrm{m} $$
 
$$ v_0 \approx 2{,}187 \cdot 10^6\,\mathrm{\frac{m}{s}}, \qquad a_0 \approx 5{,}292 \cdot 10^{-11}\,\mathrm{m} $$
 
valamint bevezettük a
 
valamint bevezettük a
26. sor: 26. sor:
 
A hidrogénatomban az elektron energiája
 
A hidrogénatomban az elektron energiája
 
$$ E_n = E_{\text{kin}\,n} + E_{\text{pot}\,n}
 
$$ E_n = E_{\text{kin}\,n} + E_{\text{pot}\,n}
−
     = \frac12 m_0 v_n^2 - \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r^2}
+
     = \frac12 m_e v_n^2 - \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r^2}
−
     = - \frac{m e^4}{2\hbar^2(4\pi\varepsilon_0)^2} \cdot \frac{1}{n^2}
+
     = - \frac{m_e e^4}{2\hbar^2(4\pi\varepsilon_0)^2} \cdot \frac{1}{n^2}
−
     = -\frac12 m_0 c^2 \alpha_f^2 \frac{1}{n^2}
+
     = -\frac12 m_e c^2 \alpha_f^2 \frac{1}{n^2}
 
     = -\frac{E_0}{n^2}, $$
 
     = -\frac{E_0}{n^2}, $$
 
ahol $E_0\approx 13{,}6\,\mathrm{eV}$ a hidrogén ionizációs energiája. A negatív előjel a kötött állapotra utal.
 
ahol $E_0\approx 13{,}6\,\mathrm{eV}$ a hidrogén ionizációs energiája. A negatív előjel a kötött állapotra utal.
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap 2013. április 23., 18:02-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Kvantummechanikai bevezető
Feladatok listája:
  1. Nap felszíni hőmérséklete
  2. Izzólámpa hatásfoka
  3. Fekete test
  4. Tantál kilépési munkája
  5. Compton-szórás
  6. Compton-szórás szabadon
  7. Fluxuskvantálás
  8. Bohr-modell
  9. Rel. tömegnövekedés
  10. Kéttest korrekció
  11. Visszalökődés
  12. Korrespondencia-elv
  13. Foton és elektron Ekin(k)
  14. Schrödinger-egyenlet
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

  1. Számítsa ki a hidrogénatom Bohr-féle modelljében a „körpályán” keringő elektron pályasugarát, sebességét, perdületét és energiáját!

Megoldás

A Bohr-féle hidrogénmodellben az elektron a rögzített atommag körül kering, impulzusmomentum a 3. posztulátum szerint kvantált, az \setbox0\hbox{$n$}% \message{//depth:\the\dp0//}% \box0%. pályán:

\[ L_n \equiv m_e v_n r_n = n\hbar. \]

A pályasugarakat és sebességeket a klasszikus képben végzet számításokból kapjuk: az atommag 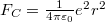\setbox0\hbox{$F_C=\frac{1}{4\pi\varepsilon_0}{e^2}{r^2}$}% \message{//depth:\the\dp0//}% \box0% Coulomb-vonzása az 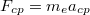\setbox0\hbox{$F_{cp}=m_e a_{cp}$}% \message{//depth:\the\dp0//}% \box0% centripetális erő, ami körpályán tartja az elektront:

\[ \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r^2} = m_e \frac{v^2}{r}. \]

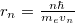\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%-rel való egyszerűsítés után beírjuk a kvantumgfeltételből kapott \setbox0\hbox{$r_n = \frac{n\hbar}{m_e v_n}$}% \message{//depth:\the\dp0//}% \box0% összefüggést, akkor a sebesség, és így a sugár lehetséges értékei rendre

\[ v_n = \frac{v_0}{n} = \alpha_f \frac{c}{n}, \qquad r_n = a_0 n^2 = \frac{n^2\hbar}{\alpha_f m_e c}, \]

ahol a legnagyobb pályasebesség és a Bohr-sugár rendre

\[ v_0 = \frac{e^2}{4\pi\varepsilon_0\hbar}, \qquad a_0 = \frac{\hbar^2 4 \pi \varepsilon_0}{m_e e^2} \]
\[ v_0 \approx 2{,}187 \cdot 10^6\,\mathrm{\frac{m}{s}}, \qquad a_0 \approx 5{,}292 \cdot 10^{-11}\,\mathrm{m} \]

valamint bevezettük a

\[ \alpha_f = \frac{e^2}{4\pi \varepsilon_0\hbar c} \approx \frac{1}{137{,}036} \]

jelölést a finomszerkezeti állandóra.

A hidrogénatomban az elektron energiája

\[ E_n = E_{\text{kin}\,n} + E_{\text{pot}\,n} = \frac12 m_e v_n^2 - \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r^2} = - \frac{m_e e^4}{2\hbar^2(4\pi\varepsilon_0)^2} \cdot \frac{1}{n^2} = -\frac12 m_e c^2 \alpha_f^2 \frac{1}{n^2} = -\frac{E_0}{n^2}, \]

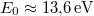ahol \setbox0\hbox{$E_0\approx 13{,}6\,\mathrm{eV}$}% \message{//depth:\the\dp0//}% \box0% a hidrogén ionizációs energiája. A negatív előjel a kötött állapotra utal.

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Kvantummechanikai_bevezető_példák_-_Bohr-féle_hidrogénmodell&oldid=9352”