„Kvantummechanikai bevezető példák - Fluxuskvantálás szemléletesen” változatai közötti eltérés
A Fizipedia wikiből
a (Szöveg koherenssé tétele) |
a |
||
| 23. sor: | 23. sor: | ||
A '''lineáris oszcillátor''' ''Lagrange''- és ''Hamilton''-függvénye rendre | A '''lineáris oszcillátor''' ''Lagrange''- és ''Hamilton''-függvénye rendre | ||
| − | $$ \mathcal{L}=\frac12 m \dot{x}^2 - \frac12 m \omega^2 x^2 | + | $$ \mathcal{L}=\frac12 m \dot{x}^2 - \frac12 m \omega^2 x^2 \qquad\text{és}\qquad \mathcal{H}=\frac{p^2}{2m} + \frac12 m \omega^2 x^2, $$ |
ahol $p=\frac{\partial \mathcal{L}}{\partial \dot{x}} = m\dot{x}$ kanonikus impulzus fázistérbeli integrálja | ahol $p=\frac{\partial \mathcal{L}}{\partial \dot{x}} = m\dot{x}$ kanonikus impulzus fázistérbeli integrálja | ||
az $E$ energiájú pályán a $\mathcal{H}=E$ egyenletű | az $E$ energiájú pályán a $\mathcal{H}=E$ egyenletű | ||
A lap 2013. május 29., 18:28-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kvantummechanikai bevezető |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Alkalmazza a Bohr-Sommerfeld-féle kvantálási hipotézist körpályán mozgó elektronra és egy lineáris oszcillátorra! Magyarázza meg a szupravezetésnél fellépő „fluxuskvantálás” jelenségét a Bohr-Sommerfeld-féle kvantálási hipotézis segítségével!
Megoldás
A Bohr-féle hidrogénmodell posztulátumai:
- Az elektron körpályán mozog (centrális erőtér).
- Megengedett pályasugarak, stacionárius pályák, ahol a töltéssel rendelkező elektron energiaveszteség nélkül keringhet (a körmozgás gyorsuló mozgás).
- A megengedett pályákon az elektron impulzusmomentuma kvantált:
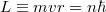(kvantumhipotézise).
- Két,
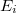és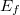 
energiájú pálya közti átmenetre a fotonkibocsátás/fotonelnyelés 
.
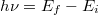A körpályán mozgó elektronra vonatkozó 3. posztulátumot úgy fogalmazhatjuk át a Lagrange-formalizmusban, hogy a rendszer Lagrange-függvénye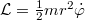 
. A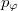 
kanonikus impulzusmomentum fázistérbeli integrálja a stacionárius pályán kvantált:
![\[ \oint p_\varphi\,\mathrm{d}\varphi = 2\pi \,p_\varphi = nh, \]](/images/math/d/8/e/d8eb8b5fa28e5360b74150d252ca9b38.png)
ahol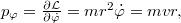 
innen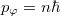 
.
A lineáris oszcillátor Lagrange- és Hamilton-függvénye rendre
![\[ \mathcal{L}=\frac12 m \dot{x}^2 - \frac12 m \omega^2 x^2 \qquad\text{és}\qquad \mathcal{H}=\frac{p^2}{2m} + \frac12 m \omega^2 x^2, \]](/images/math/b/7/8/b78c54e599964f0c3342aac79e4bbb6e.png)
ahol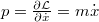 
kanonikus impulzus fázistérbeli integrálja
az 
energiájú pályán a 
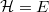egyenletű
(azaz 
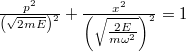egyenletű)
ellipszis területét adja. A pályaintegrál legyen az előző esethez hasonlóan kvantált:
![\[ \oint p\,\mathrm{d}x = \pi \sqrt{2mE}\sqrt{\frac{2E}{m \omega^2}} = \pi \frac{2E}{\omega} = nh, \]](/images/math/d/2/5/d259600ab9ede03f0b6848eabdce3fd2.png)
amiből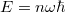 
.
