Kvantummechanikai bevezető példák - Fluxuskvantálás szemléletesen
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Stippinger (vitalap | szerkesztései) 2013. április 23., 15:47-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kvantummechanikai bevezető |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Alkalmazza a Bohr-Sommerfeld-féle kvantálási hipotézist körpályán mozgó elektronra és egy lineáris oszcillátorra! Magyarázza meg a szupravezetésnél fellépő „fluxuskvantálás” jelenségét a Bohr-Sommerfeld-féle kvantálási hipotézis segítségével!
Megoldás
A Bohr-féle hidrogénmodell kvantumhipotézisei
- az elektron körpályán mozog (centrális erőtér)
- megengedett pályasugarak, stacionárius pályák, ahol energiakisugárzás nélkül keringhet (a körmozgás gyorsuló mozgás)
- ezek a sugarak kvantáltak
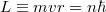
- pályák közti átmenet energiája
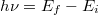
A 3. hipotézist úgy fogalmazhatjuk át a Lagrange-formalizmusban, hogy a rendszer Lagrange-függvénye 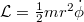 . A
. A 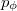 impulzusmomentum integrálja a stacionárius pályán kvantált:
impulzusmomentum integrálja a stacionárius pályán kvantált:
LaTex syntax error
\[ \oint p_\phi\,\mathrm{d}\phi = 2\pi \,\p_\phi = nh, \]
ahol 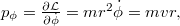 innen
innen 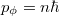 .
.