Kvantummechanikai bevezető példák - Bohr-féle hidrogénmodell kéttest korrekciója
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kvantummechanikai bevezető |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Számítsa ki, hogy a hidrogénatom Bohr-féle modelljében a mag véges nagyságú tömege milyen korrekciót jelentene az energiaszintekben és a spektrumban!
Megoldás
A kéttest korrekció alkalmazásakor a Bohr-modell tárgyalásából továbbra is érvényes, hogy a Coulomb-erő tölti be a centipetális erő szerepét
![\[ m_e \frac{v^2}{r} \equiv m_e \omega^2 r = \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r^2}, \]](/images/math/5/5/7/55738a594176a6ff37888a6aa4a66577.png)
de az impulzusmomentum kvantálását most az atommag és az elektron összes impulzusmomentumára alkalmazzuk:
![\[ m_e r_e^2 \omega + M r_M^2 \omega = n\hbar, \]](/images/math/c/5/c/c5c8c85bb1ccf4f809548f1d2b48a029.png)
ahol  az atommag tömege,
az atommag tömege, 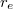 és
és 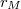 rendre az elektron és az atommag pályasugara a közös tömegközéppont körül,
rendre az elektron és az atommag pályasugara a közös tömegközéppont körül,  pedig a közös keringési körfrekvencia.
pedig a közös keringési körfrekvencia.
A tömegközéppont definíciójából
![\[ r_e = \frac{M}{m_e + M}, \qquad r_M = \frac{m_e}{m_e + M}, \]](/images/math/5/e/1/5e1b48c72410a9285ecc77c35db9c1e1.png)
ahol  az elektron és az atommag távolsága. Bevezetjük még a
az elektron és az atommag távolsága. Bevezetjük még a
![\[ \mu = \frac{m_e M}{m_e + M} \]](/images/math/c/9/f/c9f7334945bef6892a82b26ec5dd49c8.png)
redukált tömeget. Ezekkel a két egyenletünk:
![\[ \mu r_n \omega_n^2 = \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r_n^2}, \]](/images/math/f/3/e/f3e4605d2a60521506eb7a3a2e93c622.png)
![\[ \mu r_n^2 \omega_n = n\hbar, \]](/images/math/5/f/e/5fe8f1047696ecd9a73a6d3520cfe354.png)
ami a Bohr-modellével megegyező egyenletrendszer, a kéttest korrekcióval javított energiaszintek a korábbi 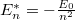 módon számolhatók az új
módon számolhatók az új
![\[ E_0^* = E_0 \frac{\mu}{m} = \frac{E_0}{1+\textstyle \frac{m_e}{M}} \approx E_0 \left(1- \frac{m_e}{M}\right) \]](/images/math/e/8/0/e802064fa27c431d6c4b66d3feba6193.png)
ionizációs energiával,
ahol 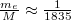 .
.
Megjegyzés
Az 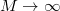 határeset visszaadja a rögzített atommag esetét, a
határeset visszaadja a rögzített atommag esetét, a 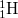 hidrogén,
hidrogén, 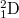 deutérium és
deutérium és 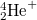 egyszeresen ionizált héliumatomon végzett kísérletekben ez az izotópeffektus mérhető, az
egyszeresen ionizált héliumatomon végzett kísérletekben ez az izotópeffektus mérhető, az 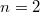 és
és 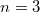 gerjesztett állapotok közötti átmenethez tartozó hullámhosszok rendre
gerjesztett állapotok közötti átmenethez tartozó hullámhosszok rendre 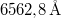 ,
, 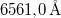 és
és 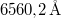 (
(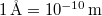 ).
).
Hélium atomban a mérést a megfelelő energiaszintek közt kell elvégezni, mert rendszáma 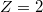 , így Coulomb-ereje is
, így Coulomb-ereje is 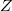 -szer nagyobb:
-szer nagyobb:
![\[ E_n^\mathrm{He} = -Z^2 \frac{E_0}{n^2} = - E_0 \frac{1}{{n^*}^2}, \]](/images/math/6/1/4/6149c543e389a2e321a7df133538d16d.png)
azaz 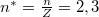 keresett hidrogénszerű állapothoz
keresett hidrogénszerű állapothoz 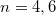 gerjesztett állapotok tartoznak.
gerjesztett állapotok tartoznak.