Kvantummechanikai bevezető példák - Izzólámpa látható tartományban kibocsátott teljesítménye
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Stippinger (vitalap | szerkesztései) 2013. április 22., 23:51-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kvantummechanikai bevezető |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy izzólámpában a volfrámszál hőmérséklete kb.
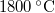 . Az emberi szem a
. Az emberi szem a 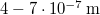 hullámhossz tartományban lát. Becsülje meg az izzólámpa „hatásfokát”!
hullámhossz tartományban lát. Becsülje meg az izzólámpa „hatásfokát”!
Megoldás
A Planck-féle sugárzási törvény szerint a fekete test által a ![\setbox0\hbox{$[\nu, \nu+\mathrm{d}\nu]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/f/c/9/fc93547493d2a6e8d98d5ee5959083a9.png) frekvenciaintervallumban kisugárzott teljesítmény
frekvenciaintervallumban kisugárzott teljesítmény
![\[ \mathcal{E}_\nu\,\mathrm{d}\nu = \frac{8\pi}{c^3} \frac{h\nu^3}{e^{\textstyle \frac{h\nu}{kT}}-1}\,\mathrm{d}\nu, \]](/images/math/b/5/6/b56bfd0a5a48ef55d0fdc2451b33a004.png)
ahol bevezetjük az 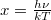 változót, és kiszámítjuk az összes kisugárzott teljesítményt:
változót, és kiszámítjuk az összes kisugárzott teljesítményt:
![\[ \mathcal{E}_t = \int_0^\infty \mathcal{E}_\nu \mathrm{d}\nu = \frac{8\pi}{c^3} \left(\frac{kT}{h}\right)^4 h \int_0^\infty \frac{x^3}{e^x-1} \,\mathrm{d}x, \]](/images/math/9/d/1/9d1a85ee14aaf403ed2bbe352ce8bc65.png)
Ahol az integrál kifejezhető a Riemann-féle 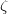 -függvénnyel, értéke
-függvénnyel, értéke 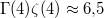 .
.
A kicsi látható ![\setbox0\hbox{$[\nu_0-\frac12\Delta\nu,\nu_0+\frac12\Delta\nu]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/4/0/3/403863cf62608e4b3637ecf4549b7308.png) tartományban kisugárzott teljesítményt közelíthetjük:
tartományban kisugárzott teljesítményt közelíthetjük:
![\[ \Delta \mathcal{E} = \mathcal{E}_{\nu_0} \Delta\nu, \]](/images/math/7/5/6/75612cbff3866be42bf2f2145971c243.png)
ahol 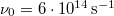 és
és 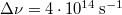 választással élünk (
választással élünk (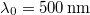 és
és 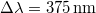 amikor a referenciaérték intervallumközép).
amikor a referenciaérték intervallumközép).
Ezekkel
![\[ \frac{\Delta \mathcal{E}}{\mathcal{E}_t} = \frac{4,976 \cdot 10^{-5}\,\mathrm{\frac{W}{m^2}}}{1,400 \cdot 10^{-2}\,\mathrm{\frac{W}{m^2}}} = 3{,}55 \cdot 10^{-3} = 0{,}355\% \]](/images/math/f/d/7/fd7fd9c182ecfe6f11433e9f5cf76b1b.png)